カーネル学習

5. カーネル学習¶

カーネル学習は分類、または回帰問題で特徴量を変換する１つの方法です。回帰問題では、以下のような回帰式を用います。

(5.1)¶\[\begin{equation} \hat{y} = \vec{w}\vec{x} + b \end{equation}\]

ここで、 \(\vec{x}\)は次元\(D\)の特徴ベクトルです。カーネル学習では次元\(D\)の特徴ベクトルから次元\(N\)の訓練データ点への距離に変換します。このときの\(N\)は訓練データ点の個数です。

(5.2)¶\[\begin{equation} \hat{y} = \sum_i^N w_i \left<\vec{x}, \vec{x}_i\right>+ b \end{equation}\]

上式の\(\left<\cdot\right>\)は２つの特徴ベクトル間の距離であり\(\vec{x}_i\)は\(i\)番目の訓練データ点です。\(\vec{x}_i\)は既知の値ですが、\(\vec{x}\)は関数の引数です。

この章の対象読者と目的

この章はRegression & Model AssessmentとClassificationに基づいて進められます。この章を修了すると

主形式と双対形式の違いを見抜けられます。
カーネル学習が上手くいきそうだと思ったときにカーネル学習をチョイスすることができます。
学習曲線の原理や訓練データサイズと特徴量の個数の間の関係を理解することができます。

この変換による帰結として、訓練データの重みベクトルが特徴量の個数に全く依存しなくなります。**その代わりに重みの個数は訓練データ点の個数に依存します。**これがカーネル学習を用いる理由になります。訓練データがほんの少ししかないのに特徴量ベクトルの次元が大きい(\(N < D\))といったことはよくあるかもしれません。カーネル定式化を使うことで重みの個数を減らすことができます。特徴空間が線形方程式でモデリングすることが困難な時でも、その特徴空間を訓練データとの距離とみなすことで線形として扱えます(多くの場合、\(N > D\))。最後に、特徴ベクトルが無限次元(i.e. ベクトルではなく関数のとき)となったり、何らかの理由で特徴ベクトルを計算できないときもあったりします。カーネル学習では、カーネル関数\(\left<\cdot\right>\)を定義する必要があるだけで特徴ベクトルを明示的に扱う必要はありません。

距離関数はカーネル関数\(\left<\cdot\right>\)と呼ばれています。カーネル関数は二変数関数（２つの引数を受け取る）であってスカラー値を出力し、以下のような性質を持ちます。

正定性(Positive): \(\left<x, x'\right> \geq 0\)
対称性(Symmetric): \(\left<x, x'\right> = \left<x', x \right>\)
Point-seperating: \(\left<x, x'\right> = 0\) if and only if \(x = x'\)

訳者注：Point-separatingにふさわしい訳語が無かったため原著の英語のみを記載した。3番目の性質に類似したものとして距離関数の定義の1つの非退化性がある。

古典的なカーネル関数の例として\(l_2\)ノルム（ユークリッド距離）があります。\(\left<\vec{x}, \vec{x}'\right>=\sqrt{\sum^D_i (x_i - x_i^{'})^2}\). 最も興味深いカーネル学習の応用の中には\(x\)がベクトルではなく関数や他の構造化されたオブジェクトであることがあります。

主形式と双対形式

双対形式とはカーネルを使うときに呼ばれるモデル式のことです。\(\hat{y} = \sum_i^N w_i \left<\vec{x}, \vec{x}_i\right>+ b\). 双対形式と区別するために通常のモデル式を主形式と言うこともできます。\(\hat{y} = \vec{w}\vec{x} + b\). 主形式もクールに聞こえますね。

カーネル学習は分子モデリングの際にポテンシャルエネルギー関数や力場を学習するための方法として広く使われています。[RTMullerVL12, SSAB20]

5.1. 溶解度の例¶

それではRegression & Model Assessmentの溶解度データセットAqqSolDB[SKE19]を再び見てみましょう。そのデータセットには水の溶解度の測定値(ラベル)と17個の分子の記述子（特徴量）をもった約10,000件のユニークな化合物があるということを思い出してください。

5.2. Notebookの実行¶

上のをクリックしてインタラクティブなGoogle Colabでこのページを開始しましょう。詳細は下記のインスト―リングパッケージを参照してください。

Tip

パッケージをインストールするには新しいセルでこのコードを実行してください。

!pip install dmol-book

もしインストールで問題があれば、このノートブックで使われている最新バージョンのパッケージを取得することができます。

いつもと同じように、下記のコードは読み込みを行っています。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import jax.numpy as jnp
import jax
import dmol

# soldata = pd.read_csv('https://dataverse.harvard.edu/api/access/datafile/3407241?format=original&gbrecs=true')
soldata = pd.read_csv(
    "https://github.com/whitead/dmol-book/raw/master/data/curated-solubility-dataset.csv"
)
features_start_at = list(soldata.columns).index("MolWt")
feature_names = soldata.columns[features_start_at:]
np.random.seed(0)

# standardize the features
soldata[feature_names] -= soldata[feature_names].mean()
soldata[feature_names] /= soldata[feature_names].std()

5.3. カーネルの定義¶

カーネル関数を作るところから始めましょう。*カーネル関数は微分可能である必要はありません。*深層学習でよく見る関数とは対照的に、カーネル法では洗練された微分不可能な関数を使うことができます。例えば、2分子間のカーネルを計算するために２成分系の分子動力学シミュレーションを用いることができます。効率性とこれまでの内容との一貫性のため、この例でもJAXを用いてカーネル関数を実装していきます。カーネルは２つの特徴ベクトルを受け取ってスカラーを返すということを思い出してください。この例では、シンプルに\(l_2\)ノルムを使います。ただ、次元数で除算することでカーネルに少しひねりを与えてやります。こうすることでカーネル関数の出力のスケールは\(x\)の次元数に依存しなくなります。

def kernel(x1, x2):
    return jnp.sqrt(jnp.mean((x1 - x2) ** 2))

5.4. モデル定義¶

ここでは、回帰モデル式を双対形式で定義します。任意の点との距離を計算するためにカーネル関数は常に訓練データを引数に持たなければならないということを思い出しましょう。新しい入力データに対して同時に全てのカーネルを計算するためにJAXのバッチ特徴量を使います。

def model(x, train_x, w, b):
    # make vectorized version of kernel
    vkernel = jax.vmap(kernel, in_axes=(None, 0), out_axes=0)
    # compute kernel with all training data
    s = vkernel(x, train_x)
    # dual form
    yhat = jnp.dot(s, w) + b
    return yhat


# make batched version that can handle multiple xs
batch_model = jax.vmap(model, in_axes=(0, None, None, None), out_axes=0)

5.5. トレーニング¶

この時点で訓練可能な重みとモデル式があります。トレーニングを始めるために、損失関数とその勾配を定義する必要があります。ここではいつもと同じように平均二乗誤差を損失関数として用います。前回見たように、正則化を利用することもできますが今のところはスキップしておきましょう。

@jax.jit
def loss(w, b, train_x, x, y):
    return jnp.mean((batch_model(x, train_x, w, b) - y) ** 2)


loss_grad = jax.grad(loss, (0, 1))


# Get 80/20 split
N = len(soldata)
train = soldata[: int(N * 0.8)]
test = soldata[int(N * 0.8) :]

# convert from pandas dataframe to numpy arrays
train_x = train[feature_names].values
train_y = train["Solubility"].values
test_x = test[feature_names].values
test_y = test["Solubility"].values

損失関数を定義し、データを訓練データとテストデータに分けました。トレーニングデータをバッチに分けることも含めて、訓練パラメーターをここで設定していきます。エポックとはデータセット全体を通しての1回のイテレーションです。

eta = 1e-5
batch_size = 32
epochs = 10


# reshape into batches
batch_num = train_x.shape[0] // batch_size
# first truncate data so it's whole nubmer of batches
trunc = batch_num * batch_size
train_x = train_x[:trunc]
train_y = train_y[:trunc]
# split into batches
x_batches = train_x.reshape(-1, batch_size, train_x.shape[-1])
y_batches = train_y.reshape(-1, batch_size)


# make trainable parameters
# w = np.random.normal(scale = 1e-30, size=train_x.shape[0])
w = np.zeros(train_x.shape[0])
b = np.mean(train_y)  # just set to mean, since it's a good first guess

学習率\(\eta\)が\(10^{-5}\)と普通より小さいことに気が付いた人がいるかもしれません。この理由はというと、約8,000個あるトレーニングデータ点のそれぞれが最後の\(\hat{y}\)に寄与しているからです。それゆえ、もし学習ステップを大きくしてしまうと\(\hat{y}\)に大きな変化を及ぼしてしまう可能性があるのです。

loss_progress = []
test_loss_progress = []

for _ in range(epochs):
    # go in random order
    for i in np.random.randint(0, batch_num - 1, size=batch_num):
        # update step
        x = x_batches[i]
        y = y_batches[i]
        loss_progress.append(loss(w, b, train_x, x, y))
        test_loss_progress.append(loss(w, b, train_x, test_x, test_y))
        grad = loss_grad(w, b, train_x, x, y)
        w -= eta * grad[0]
        b -= eta * grad[1]
plt.plot(loss_progress, label="Training Loss")
plt.plot(test_loss_progress, label="Testing Loss")

plt.xlabel("Step")
plt.yscale("log")
plt.legend()
plt.ylabel("Loss")
plt.show()

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

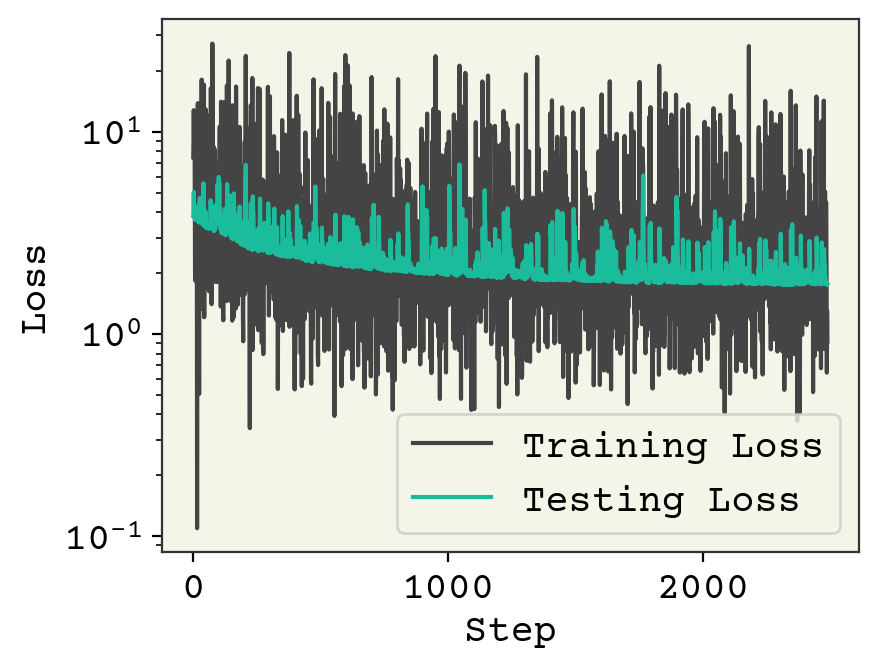
先ほどのトレーニングループとの違いはforループでバッチをランダム化したことです。

yhat = batch_model(test_x, train_x, w, b)
plt.plot(test_y, test_y, ":", linewidth=0.2)
plt.plot(test_y, yhat, "o")
plt.text(min(y) + 1, max(y) - 2, f"correlation = {np.corrcoef(test_y, yhat)[0,1]:.3f}")
plt.text(min(y) + 1, max(y) - 3, f"loss = {np.sqrt(np.mean((test_y - yhat)**2)):.3f}")
plt.title("Testing Data")
plt.show()

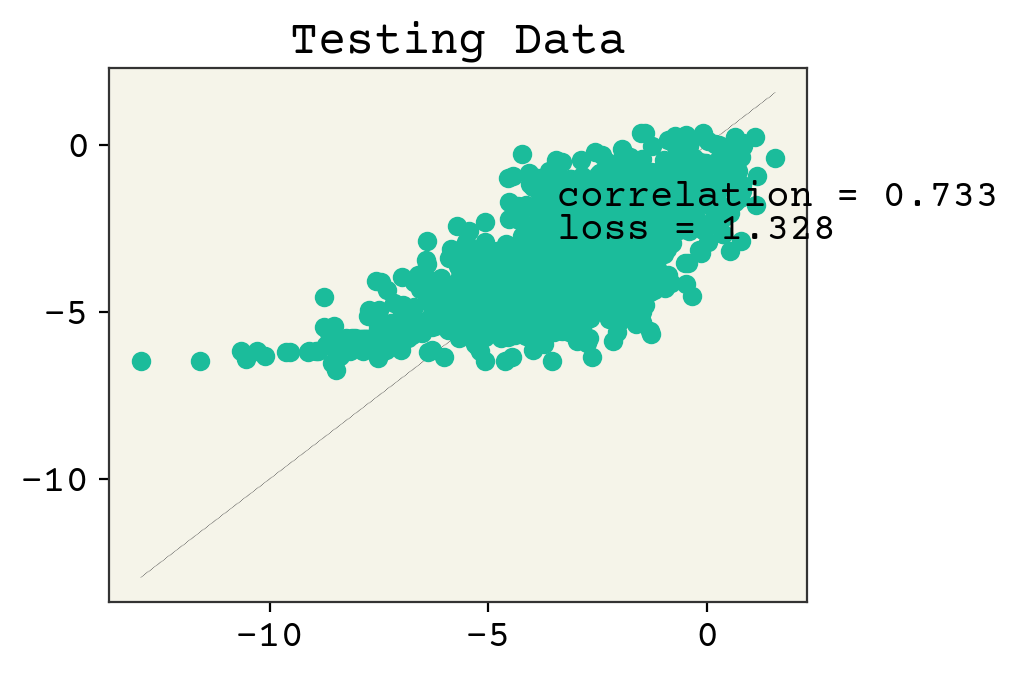
この結果は過小適合していると見受けられます。いつもと同じように、このコードを高速に実行させたいので、大きいエポック数でコードを実行しませんでした。。エポック数を増やして損失と相関が時間経過とともに改善されていくところを見ることができます。

5.6. 正則化¶

読者の中には、訓練可能なパラメーター数が意図的に訓練データ点の個数と等しくしてあることに気づいた人がいるかもしれません。もし仮に擬似逆行列を用いて回帰係数を直接計算した場合、これのせいで問題に直面することがあります。それゆえ、行列計算の解が数学的に扱いやすくできるように、そして訓練可能パラメーターが多いほうが賢明だと思われるので正則化項を追加します。線形回帰モデルで見てきたように、L1回帰はラッソ・リッジ回帰として知られ、L2回帰はカーネルリッジ回帰として知られます。L1回帰は特徴量の重要度を解釈するのに使える特定のパラメーターを洗い出すことができることを思い出してください。しかしながら、カーネル法では特定の訓練データ点との関係を示すだけで何も現実的な洞察を与えてはくれません(予測を説明する)参照)。そういうわけでカーネルリッジ回帰はカーネル法の範疇では有名です。

5.7. 学習曲線¶

（Regression & Model Assessmentのバイアス-バリアンストレードオフは、モデルの複雑さを増加させると、モデルのバリアンス（トレーニングデータの選択の仕方と量により強く影響を受ける）の増加を犠牲にしてどれほどモデルのバイアス（より表現力が高く、より良くデータに適合できる）を軽減できるかについて示しました。モデルの複雑さは特徴量の個数を調整することによって制御することができました。カーネル法では特徴量の個数をコントロールしません。というのもそれが訓練データ点の個数と常に一致するからです。それゆえ、カーネルの選択や正則化、学習率などのようなハイパーパラメーターをコントロールするだけになります。このハイパーパラメーターの効果を評価するためにテストの損失を計算するだけでは終わることはできません。なぜならその損失がトレーニングデータの量に強く関係しているからです。多くの訓練データがあるということはモデルがより洗練されるということを意味し、損失の値が減少します。なので、とりわけカーネル学習ではトレーニングデータの量に対してテスト損失の値がどれほど変わるのかを示すということは常識的なことです。値が大きなスケールで変化するのでこれらは対数-対数プロットで示されます。これらは学習曲線(もしくはLearning curves)と呼ばれています。学習曲線は機械学習や深層学習で広く使われていますが、カーネル学習でも頻繁に見ることになります。

溶解度のモデルに再び戻って学習曲線を用いてL1とL2の正則化を比較してみましょう。注意しておきますが、\(M\)個のモデル（\(M\)は学習曲線で取得したい点の個数）を計算しなければならないので、このコードは非常に遅くなります。このテキストでは効率性を保つために学習曲線上の点として数個を用いることにします。

最初にトレーニングの過程を関数にまとめます。

def fit_model(loss, npoints, eta=1e-6, batch_size=16, epochs=25):

    sample_idx = np.random.choice(
        np.arange(train_x.shape[0]), replace=False, size=npoints
    )
    sample_x = train_x[sample_idx, :]
    sample_y = train_y[sample_idx]

    # reshape into batches
    batch_num = npoints // batch_size
    # first truncate data so it's whole nubmer of batches
    trunc = batch_num * batch_size
    sample_x = sample_x[:trunc]
    sample_y = sample_y[:trunc]
    # split into batches
    x_batches = sample_x.reshape(-1, batch_size, sample_x.shape[-1])
    y_batches = sample_y.reshape(-1, batch_size)

    # get loss grad
    loss_grad = jax.grad(loss, (0, 1))

    # make trainable parameters
    # w = np.random.normal(scale = 1e-30, size=train_x.shape[0])
    w = np.zeros(sample_x.shape[0])
    b = np.mean(sample_y)  # just set to mean, since it's a good first guess
    for _ in range(epochs):
        # go in random order
        for i in np.random.randint(0, batch_num - 1, size=batch_num):
            # update step
            x = x_batches[i]
            y = y_batches[i]
            grad = loss_grad(w, b, sample_x, x, y)
            w -= eta * grad[0]
            b -= eta * grad[1]
    return loss(w, b, sample_x, test_x, test_y)


# test it out
fit_model(loss, 256)

DeviceArray(3.8454313, dtype=float32)

ここでは私たち専用のL1とL2バージョンの損失関数を作っていきます。正則化の*強度(strength)*を選択しなければなりません。重みは1より小さいのでL2に対してはよりもっと強い正則化の強度を選択することにします。これらはハイパーパラメーターですがフィッティングを向上させるために調整しても問題ないです。

@jax.jit
def loss_l1(w, b, train_x, x, y):
    return jnp.mean((batch_model(x, train_x, w, b) - y) ** 2) + 1e-2 * jnp.sum(
        jnp.abs(w)
    )


@jax.jit
def loss_l2(w, b, train_x, x, y):
    return jnp.mean((batch_model(x, train_x, w, b) - y) ** 2) + 1e2 * jnp.sum(w**2)

そして、学習曲線に必要な点を生成します！

nvalues = [32, 256, 512, 1024, 2048, 1024 * 5]

nor_losses = [fit_model(loss, n) for n in nvalues]
l1_losses = [fit_model(loss_l1, n) for n in nvalues]
l2_losses = [fit_model(loss_l2, n) for n in nvalues]

plt.plot(nvalues, nor_losses, label="No Regularization")
plt.plot(nvalues, l1_losses, label="L1 Regularization")
plt.plot(nvalues, l2_losses, label="L2 Regularization")
plt.legend()
plt.xlabel("Training Data Amount")
plt.ylabel("Test Loss")
plt.gca().set_yscale("log")
plt.gca().set_xscale("log")

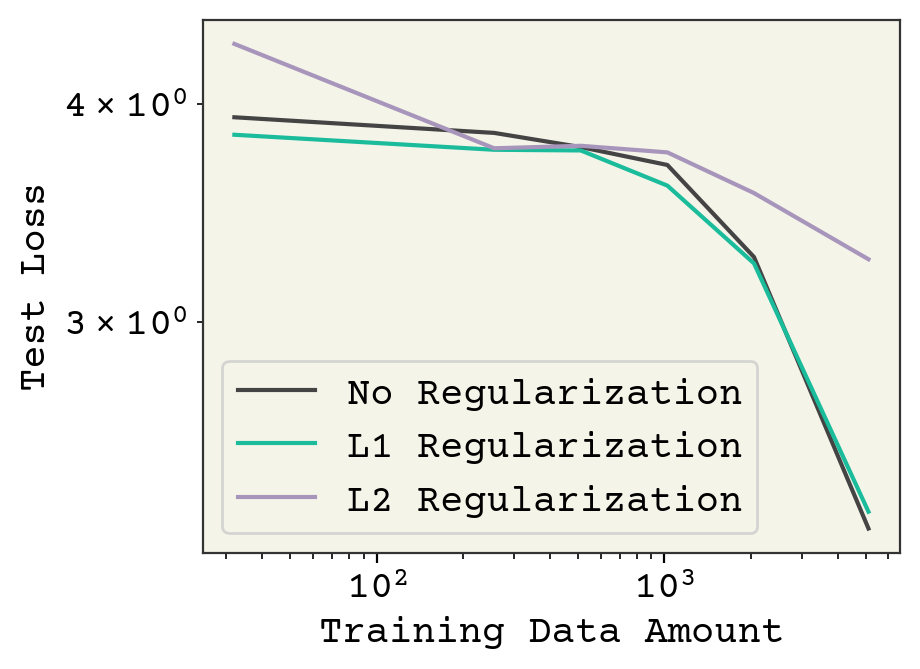
最後に別々のアプローチをとった学習曲線を見てみましょう。正則化はテストデータの最終的な損失になにかしらの影響を及ぼしています。L1とL2正則化は単純に悪くなっているかの是非や正則化の強度をもっと調整したほうが良いかどうかについて言及することは困難です。とは言え、このプロットを見る限りでは我々がカーネル学習法を典型的な方法で評価したということはわかります。

5.8. 練習問題¶

双対形式の回帰式から勾配を計算し、その計算結果を用いてカーネル関数がなぜ微分可能である必要がないのかについて説明しなさい。
カーネル学習でトレーニングを行うと速いか遅いか？説明しなさい。
カーネル学習で予測するのは速いか遅いか？説明しなさい。
分類タスクを行うために式4.2をどのように修正すればよいか？
カーネルの種類に関わらず、重みの値がトレーニングデータの相対的な重要度を示しているだろうか？
上記の例からL1正則化の強度が異なる5つの学習曲線を作成しなさい。この例で正則化が意味をなさないのないのはなぜか？

5.9. 章のまとめ¶

この章ではカーネル学習を紹介した。カーネル学習は特徴量をサンプル間の距離に変換する方法である。
カーネル関数は2つの引数を受け取ってスカラーを出力する。カーネル関数は3つの性質を持たなければならない（正定性(positive)・対称性(symmetry)・Point-separating）。）
距離関数（内積）はカーネル関数である。
カーネル関数は微分可能である必要はない。
カーネル学習は二変数カーネル関数だけで定められる特徴量を使いたいときに相応しい手法である。
カーネルモデルの訓練可能パラメーターの個数は特徴量の次元数ではなく訓練データ点の個数に比例する。

5.10. Cited References¶

SKE19: Murat Cihan Sorkun, Abhishek Khetan, and Süleyman Er. AqSolDB, a curated reference set of aqueous solubility and 2D descriptors for a diverse set of compounds. Sci. Data, 6(1):143, 2019. doi:10.1038/s41597-019-0151-1.
SSAB20: Christoph Scherer, René Scheid, Denis Andrienko, and Tristan Bereau. Kernel-based machine learning for efficient simulations of molecular liquids. Journal of Chemical Theory and Computation, 16(5):3194–3204, 2020.
RTMullerVL12: Matthias Rupp, Alexandre Tkatchenko, Klaus-Robert Müller, and O Anatole Von Lilienfeld. Fast and accurate modeling of molecular atomization energies with machine learning. Physical review letters, 108(5):058301, 2012.

4. Classification

6. ディープラーニングの概要

deep learning for molecules & materials