ディープラーニングの概要

6. ディープラーニングの概要¶

ディープラーニング は、 機械学習のカテゴリの一つです。また機械学習は 人工知能（AI） のカテゴリの一つです。ディープラーニングは、ニューラルネットワークを用いて回帰や分類のような機械学習を実現します。まずこの章ではディープラーニングの概要を紹介し、この後の章でさらに詳細に踏み込んでいきます。

読者と & 目的

本章は Regression & Model Assessment および機械学習入門の内容を前提とします。本章を通じて、あなたは次のことを学ぶでしょう：

ディープラーニングの定義
ニューラルネットワークの定義
これまでに学んだ回帰の原理のニューラルネットワークへの応用

この本の目的は、化学および材料科学を中心としたディープラーニングの入門書となることです。ディープラーニングに関しては、本書の他に数多くの優れた資料があり、ここでそれらの一部に触れておくことにします。これらのリソースでは、特定のトピックについてのより詳細な説明や、本書で扱わないトピック（例えば、画像認識）についての説明がなされています。まずディープラーニングの入門に関しては、Ian Goodfellowの本が良い入門書だと思いました。ビジョンについて深く知りたいなら、Grant Sandersonがニューラルネットワークに特化したshort video seriesを公開しており、このトピックの応用的な紹介がされています。DeepMindは、ディープラーニングとAIで何が実現できるかを示すハイレベルなビデオを公開しています。もし研究論文で「ディープラーニングは強力なツールである」と書く場合、一般的にはヤン・ルカン、ヨシュア・ベンジオ、ジェフリー・ヒントンにより執筆されNatureに掲載された [この論文] (https://www.nature.com/articles/nature14539)が引用されることが多いでしょう。Zhang、 Lipton、 Li、および Smolaは、Tensorflow、PyTorch、MXNetといった代表的なディープラーニングフレームワークで実装されたexampleを含む実用的なオンラインブックを公開しています。また、DeepChemプロジェクトでは、化学におけるディープラーニングの応用について、化学にフォーカスした多くのexampleと情報が提供されています。最後に、いくつかのディープラーニングパッケージは、そのAPIのチュートリアルを介して深層学習の短い導入を提供します： Keras, PyTorch.

私がディープラーニングの初心者に伝える主なアドバイスは、神経学に着想を得た用語や概念（すなわち、ニューロン間の接続）にはあまり囚われすぎず、その代わりにディープラーニングを、調整可能なパラメータをたくさん含む行列を使った一連の線形代数演算として捉えることです。もちろん、ディープラーニングの線形代数演算を結合するために使われる非線形関数（活性化）など、神経学と類似した概念もところどころに登場しますが、ニューラルネットワークは神経学の延長にあるものではなく、それとは切り離された別なものとして学ぶことが適切と言えます。例え脳内で接続されたニューロンのように見えたとしても―――ディープラーニングは本質的に、「計算ネットワーク」（計算グラフとも呼ばれる）によって記述される線形代数演算です。

非線形性

関数 \(f(\vec{x})\) が次の2つの条件を満たすなら、\(f(\vec{x})\)は線形である：

任意の \(\vec{x}\) および \(\vec{y}\) について、

(6.1)¶\[\begin{equation} f(\vec{x} + \vec{y}) = f(\vec{x}) + f(\vec{y}) \end{equation}\]

また、

(6.2)¶\[\begin{equation} f(s\vec{x}) = sf(\vec{x}) \end{equation}\]

ここで \(s\) はスカラーである。もし\(f(\vec{x})\)がこれらの条件を満たさない場合、\(f(\vec{x})\)は 非線形 である。

6.1. ニューラルネットワークとは？¶

ディープラーニングにおける ディープ とは、ニューラルネットワークが何層ものレイヤーから構成されることを意味します。では、ニューラルネットワークとは何でしょうか？一般化した言い方をすれば、ニューラルネットワークは2つの要素で構成されると考えることができます：（1）入力特徴 \(\mathbf{X}\) に対して非線形変換 \(g(\cdot)\) を適用し、新しい特徴 \(\mathbf{H} = g(\mathbf{X})\) を出力する部分、（2）既に機械学習入門で見たような線形モデル。我々のディープラーニングによる回帰モデルの式は次のようになっています。

(6.3)¶\[\begin{equation} \hat{y} = \vec{w}g(\vec{x}) + b \end{equation}\]

MLの章では、特徴量の選択がいかに難解かつ困難かという点が主に議論されてきました。ここでは、これまで人手で設計されてきた特徴量を、学習可能な特徴の集合 \(g(\vec{x})\) に置き換え、これまでと同じ線形モデルを使います。それでは \(g(\vec{x})\) はどのように設計すればよいのかと気になるでしょうが、これがまさにディープラーニングの部分です。 \(g(\vec{x})\) は レイヤー（層） によって構成される微分可能な関数で、層それ自身も微分可能かつ、学習可能な重み（自由変数）を持ちます。ディープラーニングは成熟した分野であり、目的ごとに標準的な層が確立されています。例えば、畳み込み層は、入力テンソルの各要素の周辺について、固定された広さで近傍を見るために使われ、ドロップアウト層は、正則化の一種として入力ノードをランダムに不活性化するために使われます。最もよく使われる基本的な層は、全結合層（fully-connected layer） あるいは 密結合層（dense layer） と呼ばれるものです（訳注：以下の説明で、原文ではdense layerの呼称が使われていますが、日本語では全結合層としています）。

全結合層は、所望の出力特徴のshapeと活性化の2つで定義されます。全結合層の式は次のようになります：

(6.4)¶\[\begin{equation} \vec{h} = \sigma(\mathbf{W}\vec{x} + \vec{b}) \end{equation}\]

ここで、\(\mathbf{W}\) は学習可能な \(D \times F\) 行列、\(D\) は入力ベクトル (\(vec{x}\)) の次元、\(F\) は出力ベクトル (\(vec{h}\)) の次元、\(vec{b}\) は学習可能な \(F\) 次元ベクトル、\(\sigma(\cdot)\) は活性化関数です。出力特徴数の \(F\) や \(\sigma(\cdot)\) はこのモデルのハイパーパラメータの一つで、つまりモデルの学習時に自動的に獲得される値ではなく、問題ごとにチューニングすべき値です。活性化関数には、微分可能かつ値域が \((-\infty, \infty)\) であれば、基本的にどのような関数も使用できます。ただし、活性化関数が線形関数の場合、複数の全結合層を重ねたとしても単に行列を定数倍したことと等価であり、結局のところ線形回帰になってしまいます。よって、ニューラルネットワークが非線形性をもつ関数を表現できるよう、活性化関数には非線形な関数を用いるのが普通です。また非線形性だけでなく、活性化関数はオン・オフが可能、つまり、入力値のある領域に対して出力値が0になる性質が必要です。一般に、負の入力に対して活性化関数はゼロもしくはそれに近い値になります。

これら2つの性質を備えた最もシンプルな活性化関数は、正規化線形関数（rectified linear unit, ReLU)で、以下のように表されます：

\[\begin{split} \sigma(x) = \left\{\begin{array}{lr} x & x > 0\\ 0 & \textrm{otherwise}\\ \end{array}\right. \end{split}\]

6.1.1. 万能近似定理¶

ニューラルネットワークが未知関数 (\(f(\vec{x})\)) の近似に適している理由の一つは、ネットワークの深さ（層の数）や幅（隠れ層の大きさ）が十分に大きければ、どんな関数でも近似できることです（万能近似定理）。この定理には多くのバリエーションがあり、無限に広いニューラルネットや無限に深いニューラルネットについての証明が示されています。例えば、任意の1次元の関数は、無限に広い層（無限の隠れ層次元）を持ち活性化関数としてReLUが用いられた、深さ5のニューラルネットワークで近似できることが知られています[LPW+17]。

6.1.2. Frameworks¶

ディープラーニングの実装には、多くの「ハマりポイント」（※）、つまり容易にミスを犯してしまうポイントがたくさんあるため、ニューラルネットワークや学習に必要な様々な機能を自分でゼロから実装することは難しいです。特に数値的な不安定性は、モデルが学習に失敗した時にはじめて気づく場合が多く、厄介な問題になります。そこでこの本のいくつかの例では、JAXの代わりに少し抽象的なソフトウェアフレームワークを用いることにします。ここでは、人気のあるディープラーニングフレームワークの1つであるKerasを用います。Kerasは高度な処理を非常にシンプルなコードで記述できることから、ディープラーニングの実例を簡潔に示すために適していると言えます。

6.1.3. ディスカッション¶

この本では、ディープラーニングそのものの紹介はなるべくあっさりと済ませます。世の中にはディープラーニングに関する優れた学習教材があります。上記の読み物や、Keras（またはPyTorch）のチュートリアルを使って、ニューラルネットワークや学習の概念に慣れておくとよいでしょう。

6.2. 溶解度予測モデルを振り返る¶

ディープラーニングの最初の例として、2層の全結合ニューラルネットワークを使って溶解度データセットを再度学習してみましょう。

6.3. このノートブックの動かし方¶

このページ上部のを押すと、このノートブックがGoogle Colab.で開かれます。必要なパッケージのインストール方法については以下を参照してください。

Tip

必要なパッケージをインストールするには、新規セルを作成して次のコードを実行してください。

!pip install dmol-book

もしインストールがうまくいかない場合、パッケージのバージョン不一致が原因である可能性があります。動作確認がとれた最新バージョンの一覧はここから参照できます

import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
import dmol

6.3.1. データの読み込み¶

データをダウンロードし、Pandasのdata frameとして読み込みます。さらに、以前と同じようにして特徴量を正規化します。

# soldata = pd.read_csv('https://dataverse.harvard.edu/api/access/datafile/3407241?format=original&gbrecs=true')
# had to rehost because dataverse isn't reliable
soldata = pd.read_csv(
    "https://github.com/whitead/dmol-book/raw/master/data/curated-solubility-dataset.csv"
)
features_start_at = list(soldata.columns).index("MolWt")
feature_names = soldata.columns[features_start_at:]
# standardize the features
soldata[feature_names] -= soldata[feature_names].mean()
soldata[feature_names] /= soldata[feature_names].std()

6.4. Keras用にデータを準備¶

ディープラーニングライブラリを使うことで、データの分割や各レイヤーの構築など、多くの一般的タスクが簡単に行えます。以下のコードでは、numpyのarrayからKerasのデータセットを構築します。

full_data = tf.data.Dataset.from_tensor_slices(
    (soldata[feature_names].values, soldata["Solubility"].values)
)
N = len(soldata)
test_N = int(0.1 * N)
test_data = full_data.take(test_N).batch(16)
train_data = full_data.skip(test_N).batch(16)

このコード内における skip や take (次を参照 tf.data.Dataset) は、データセットを2つに分割し、ミニバッチを作る操作です。

6.5. ニューラルネットワーク¶

では、ニューラルネットワークモデルを構築しましょう。この場合、 \(g(\vec{x}) = \sigma\left(\mathbf{W^0}\vec{x} + \vec{b}\right)\) となります。この関数 \(g(\vec{x})\) を 隠れ層（hidden layer） と呼ぶことにします。これは、我々は \(g(\vec{x})\) の出力をそのまま最終的な結果として扱うわけではないからです。予測したい溶解度は \(y = \vec{w}g(\vec{x}) + b\) となることに注意してください。活性化関数 \(sigma( \cdot)\) はtanh、隠れ層の出力次元は32とします。非線形な活性化関数はたくさんありますが、ここでtanhを選んだのは経験的な理由です。このように、活性化関数は一般的に効率と経験的な性能に基づいて選択されます。

# our hidden layer
# We only need to define the output dimension - 32.
hidden_layer = tf.keras.layers.Dense(32, activation="tanh")
# Last layer - which we want to output one number
# the predicted solubility.
output_layer = tf.keras.layers.Dense(1)

# Now we put the layers into a sequential model
model = tf.keras.Sequential()
model.add(hidden_layer)
model.add(output_layer)

# our model is complete

# Try out our model on first few datapoints
model(soldata[feature_names].values[:3])

<tf.Tensor: shape=(3, 1), dtype=float32, numpy=
array([[-0.19586785],
       [-0.41813114],
       [-0.11751032]], dtype=float32)>

上の3つの分子に対する溶解度を予測するモデルができました。Pandasのデータはデータ精度にfloat64（倍精度浮動小数点）を使っているのに、我々のモデルはfloat32（単精度）を使っているという警告が出るかもしれませんが、これはそれほど重要ではありません。この警告は技術的理由から数値の精度を少し落としているためですが、分子の溶解度は32ビットと64ビット精度の浮動小数点による誤差よりもはるかに多くの分散を持っていることから、この誤差の影響は無視できます。最後の行を次のように修正すれば、この警告を消すことができます。

model(soldata[feature_names].values[:3].astype(float))

ここまでで、我々はディープニューラルネットワークのモデル構造を目的に従って定義し、データに対して呼び出すことができるようになりました。あとはこのモデルを学習させるだけです。model.compile を呼び出し、最適化器（通常は確率的勾配降下法の一種）と損失関数を定義することで、学習用モデルの準備は完了です。

model.compile(optimizer="SGD", loss="mean_squared_error")

Kerasを使うと簡単にディープラーニングモデルが定義できることに気づきましたか？以前に損失と最適化器を準備するためにかかった労力を振り返ってみてください。これがディープラーニングフレームワークを使う利点です。では、これでモデルを学習するための準備が整いました。

model.fit(train_data, epochs=50)

学習も簡単ですね！

参考までに、前回のベースラインモデルではlossの出力は3くらいでした。また、Kerasによる最適化により、処理はより高速になりました。では、このモデルのテストデータにおける性能を見てみましょう。

# get model predictions on test data and get labels
# squeeze to remove extra dimensions
yhat = np.squeeze(model.predict(test_data))
test_y = soldata["Solubility"].values[:test_N]

plt.plot(test_y, yhat, ".")
plt.plot(test_y, test_y, "-")
plt.xlabel("Measured Solubility $y$")
plt.ylabel("Predicted Solubility $\hat{y}$")
plt.text(
    min(test_y) + 1,
    max(test_y) - 2,
    f"correlation = {np.corrcoef(test_y, yhat)[0,1]:.3f}",
)
plt.text(
    min(test_y) + 1,
    max(test_y) - 3,
    f"loss = {np.sqrt(np.mean((test_y - yhat)**2)):.3f}",
)
plt.show()

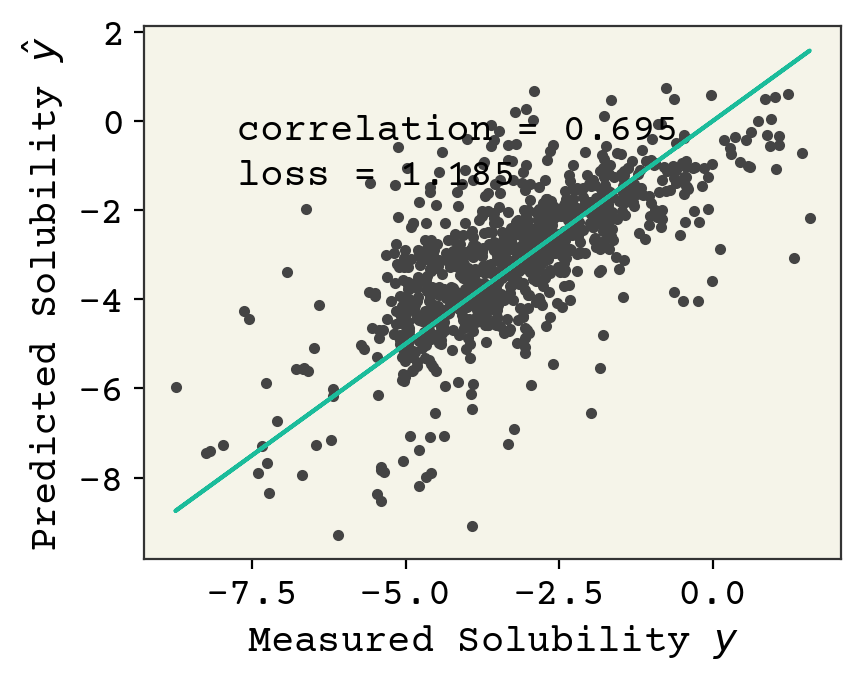
性能も、ベースラインモデルよりかなり良いことがわかりｍす。 This performance is better than our simple linear model.

6.6. 練習問題¶

ReLU関数をグラフにプロットし、ReLUが非線形関数であることを確認せよ
バイアス・バリアンストレードオフのことは一旦忘れて、ニューラルネットワークの層の数を増やすことにチャレンジしてみてください
\(\sigma(\cdot)\) が恒等関数であれば、ニューラルネットワークは線形回帰であることを示せ。
データのフィッティングに、非線形回帰ではなく、ディープラーニングを使うメリットとデメリットは何ですか？また、どのような場合にディープラーニングではなく非線形回帰を選択しますか？

6.7. この章の目次¶

ディープラーニングとは、機械学習の一種で、ニューラルネットワークを利用してデータの分類や回帰を行うものです。
ニューラルネットワークは、調整可能なパラメータを持つ行列を用いた一連の演算です。
ニューラルネットワークは、入力された特徴を、その後回帰や分類に使用できる新しい特徴の集合に変換します。
最も一般的な層は全結合層で、全結合層において各入力要素は各出力要素に影響を与えます。全結合層のパラメータは望ましい出力特徴の形と活性化関数によって定義されます。
十分な数の層、または十分な幅の隠れ層があれば、ニューラルネットワークは未知の関数を近似することができます。
隠れ層は、その出力を我々は普段観測しないため、このように呼ばれています。
TensorFlowなどのライブラリを使うと、データをトレーニングとテストに分けるだけでなく、ニューラルネットワークの層を構築することも容易になります。
ニューラルネットワークを構築することで、分子の溶解度など様々な物性を予測することができます。

6.8. Cited References¶

LPW+17: Zhou Lu, Hongming Pu, Feicheng Wang, Zhiqiang Hu, and Liwei Wang. The expressive power of neural networks: a view from the width. In Proceedings of the 31st International Conference on Neural Information Processing Systems, 6232–6240. 2017.

5. カーネル学習

7. Standard Layers

deep learning for molecules & materials