機械学習入門

2. 機械学習入門¶

機械学習入門と呼ばれる記事は、おそらくwebサイト上に数千件あります。本稿では、これらの記事を書き直すのではなく、化学での応用に焦点を当てた主要な概念を紹介することにします。以下に入門的な資料を挙げます。新しいより良いものがほかにあれば教えてください。

原著者が大学院で初めて読んだ、機械学習についてのEthem Alpaydinによって書かれた本[Alp20]
Nils Nillsonのオンラインブック Introductory Machine Learning
物質科学における機械学習についての2つのreview[FZJS21, Bal19]
計算科学における機械学習についての2つのreview[GomezBAG20]
金属科学における機械学習についての2つのreview[NDJ+18]

これらの資料から、機械学習がデータをモデリングする手法であり、一般的にはには予測機能を持つことを学んでいただけると思います。機械学習には多くの手法が含まれますが、ここでは深層学習を学ぶために必要なものだけを取り上げます。例えば、ランダムフォレスト、サポートベクターマシン、最近傍探索などは広く使われている機械学習手法で、今でも有効な手法ですが、ここでは取り上げません。

読者層と目的

本章は、化学とpythonについてある程度知識のある機械学習の初心者を対象としており、そうでない場合には上記の入門記事のいずれかに目を通しておくことをお勧めします。この記事では、pandasの知識（カラムの読み込みと選択）、rdkitの知識（分子の描き方）、分子をSMILES [Wei88]として保存する方法についてある程度の知識を想定しています。この章を読むと、以下のことができるようになると想定されます。

特徴量、ラベルの定義
教師あり学習と教師なし学習を区別できる。
損失関数とは何か、勾配降下法を用いてどのように最小化できるかを理解する。
モデルとは何か、特徴とラベルとの関係を理解する。
データのクラスタリングができ、それがデータについて何を示すかを説明できる。

2.1. 用語の説明¶

機械学習とは、データに当てはめてモデルを構築することを目指す分野です。まず、言葉を定義します。

特徴量

次元\(D\)の\(N\)個のベクトル \(\{\vec{x}_i\}\) の集合です。実数、整数等が用いられます。

ラベル

\(N\) 個の整数または実数の集合 \(\{y_i\}\)。\(y_i\) は通常スカラーです。

ラベル付きデータ

\(N\) 個のtupleからなる集合 \(\{\left(\vec{x}_i, y_i\right)\}\) を指します。

ラベルなしデータ

ラベル \(y\) が未知の \(N\) 個の特徴量 \(\{\vec{x}_i\}\) の集合を指します。

モデル

特徴ベクトルを受け取り、予測結果 \(\hat{y}\) を出力する関数 \(f(\vec{x})\) を指します。

予測結果

与えられた入力 \(\vec{x}\) に対し、モデルを通して得られた予測結果 \(\hat{y}\) のことを指します。

2.2. 教師あり学習¶

最初のタスクは教師あり学習です。教師あり学習とは、データで学習したモデルで \(\vec{x}\) から \(y\) を予測する方法です。このタスクは、データセットに含まれるラベルをアルゴリズムに教えることで学習を進めるため、教師あり学習と呼ばれています。もう一つの方法は教師なし学習で、アルゴリズムにラベルを教えない方法です。この教師あり／教師なしの区別は後でもっと厳密になりますが、今のところはこの定義で十分です。

例として、AqSolDB[SKE19]という、約1万種類の化合物と、その水への溶解度の測定結果(ラベル)についてのデータセットを使ってみます。このデータセットには、機械学習に利用できる分子特性（特徴量）も含まれています。溶解度の測定結果は、化合物の水への溶解度をlog molarityの単位で表したものになります。

2.3. Notebookの実行¶

上にあるをクリックすると、このページがインタラクティブなGoogle Colab Notebookとして起動されるようになります。パッケージのインストールについては、以下を参照してください。

Tip

パッケージをインストールするには、新しいセルで次のコードを実行します。

!pip install dmol-book

インストールに問題が生じた場合は、このリンクから使用されているパッケージリストの最新版を入手することができます。

2.3.1. データのロード¶

データをダウンロードし、Pandasのデータフレームにロードします。以下のセルでは、インポートや必要なパッケージのインストールを設定します。

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import jax.numpy as jnp
import jax
from jax.example_libraries import optimizers
import sklearn.manifold, sklearn.cluster
import rdkit, rdkit.Chem, rdkit.Chem.Draw
import dmol

# soldata = pd.read_csv('https://dataverse.harvard.edu/api/access/datafile/3407241?format=original&gbrecs=true')
# had to rehost because dataverse isn't reliable
soldata = pd.read_csv(
    "https://github.com/whitead/dmol-book/raw/master/data/curated-solubility-dataset.csv"
)
soldata.head()

	ID	Name	InChI	InChIKey	SMILES	Solubility	Ocurrences	Group	MolWt	...	NumRotatableBonds	NumValenceElectrons	NumAromaticRings	NumSaturatedRings	NumAliphaticRings	RingCount	TPSA	LabuteASA	BalabanJ	BertzCT
0	A-3	N,N,N-trimethyloctadecan-1-aminium bromide	InChI=1S/C21H46N.BrH/c1-5-6-7-8-9-10-11-12-13-...	SZEMGTQCPRNXEG-UHFFFAOYSA-M	[Br-].CCCCCCCCCCCCCCCCCC[N+](C)(C)C	-3.616127	1	G1	392.510	...	17.0	142.0	0.0	0.0	0.0	0.0	0.00	158.520601	0.000000e+00	210.377334
1	A-4	Benzo[cd]indol-2(1H)-one	InChI=1S/C11H7NO/c13-11-8-5-1-3-7-4-2-6-9(12-1...	GPYLCFQEKPUWLD-UHFFFAOYSA-N	O=C1Nc2cccc3cccc1c23	-3.254767	1	G1	169.183	...	0.0	62.0	2.0	0.0	1.0	3.0	29.10	75.183563	2.582996e+00	511.229248
2	A-5	4-chlorobenzaldehyde	InChI=1S/C7H5ClO/c8-7-3-1-6(5-9)2-4-7/h1-5H	AVPYQKSLYISFPO-UHFFFAOYSA-N	Clc1ccc(C=O)cc1	-2.177078	1	G1	140.569	...	1.0	46.0	1.0	0.0	0.0	1.0	17.07	58.261134	3.009782e+00	202.661065
3	A-8	zinc bis[2-hydroxy-3,5-bis(1-phenylethyl)benzo...	InChI=1S/2C23H22O3.Zn/c2*1-15(17-9-5-3-6-10-17...	XTUPUYCJWKHGSW-UHFFFAOYSA-L	[Zn++].CC(c1ccccc1)c2cc(C(C)c3ccccc3)c(O)c(c2)...	-3.924409	1	G1	756.226	...	10.0	264.0	6.0	0.0	0.0	6.0	120.72	323.755434	2.322963e-07	1964.648666
4	A-9	4-({4-[bis(oxiran-2-ylmethyl)amino]phenyl}meth...	InChI=1S/C25H30N2O4/c1-5-20(26(10-22-14-28-22)...	FAUAZXVRLVIARB-UHFFFAOYSA-N	C1OC1CN(CC2CO2)c3ccc(Cc4ccc(cc4)N(CC5CO5)CC6CO...	-4.662065	1	G1	422.525	...	12.0	164.0	2.0	4.0	4.0	6.0	56.60	183.183268	1.084427e+00	769.899934

5 rows × 26 columns

2.3.2. データ探索¶

分子には、分子量、回転可能な結合、価電子など、様々な特徴量となりうるものがあります。そしてもちろん、今回のデータセットにおいてラベルとなる溶解度という指標もあります。このデータセットに対して私たちが常に最初に行うべきことの一つは、探索的データ解析（EDA）と呼ばれるプロセスでデータについての理解を深めることです。まず、ラベルやデータの大枠を知るために、いくつかの具体的な例を調べることから始めましょう。

# plot one molecule
mol = rdkit.Chem.MolFromInchi(soldata.InChI[0])
mol

これはデータセットのうち、最初の分子をrdkitを使ってレンダリングしたものです。

それでは、溶解度データの範囲とそれを構成する分子についてなんとなく理解するために、極値を見てみましょう。まず、溶解度の確率分布の形と極値を知るために、(seaborn.distplot を使って)溶解度のヒストグラムを作成します。

sns.distplot(soldata.Solubility)
plt.show()

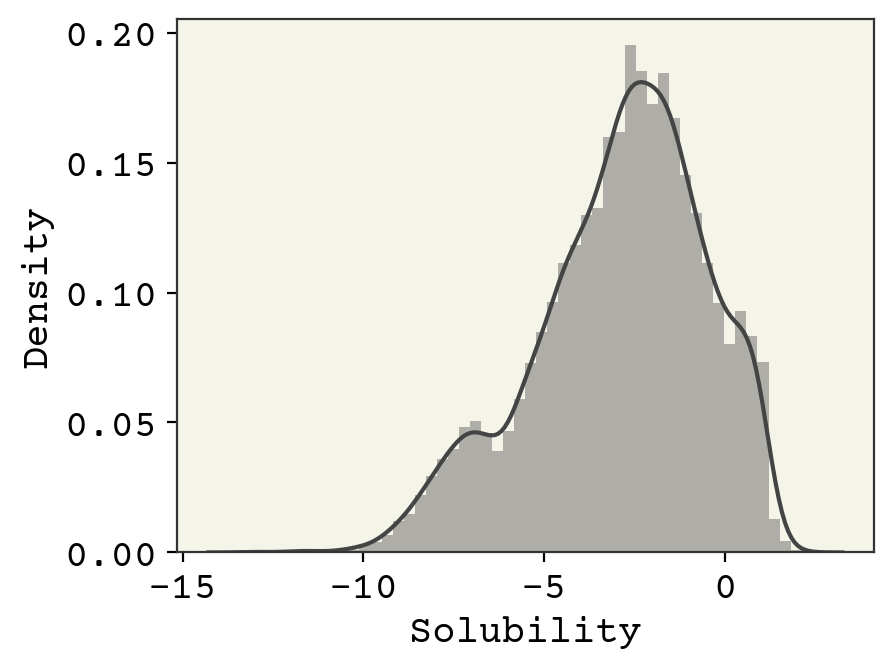
上図では、溶解度のヒストグラムとカーネル密度推定値を重ね合わせています。このヒストグラムから、溶解度は約-13から2.5まで変化し、正規分布していないことがわかります。

# get 3 lowest and 3 highest solubilities
soldata_sorted = soldata.sort_values("Solubility")
extremes = pd.concat([soldata_sorted[:3], soldata_sorted[-3:]])

# We need to have a list of strings for legends
legend_text = [
    f"{x.ID}: solubility = {x.Solubility:.2f}" for x in extremes.itertuples()
]

# now plot them on a grid
extreme_mols = [rdkit.Chem.MolFromInchi(inchi) for inchi in extremes.InChI]
rdkit.Chem.Draw.MolsToGridImage(
    extreme_mols, molsPerRow=3, subImgSize=(250, 250), legends=legend_text
)

極端な分子の例では、高塩素化合物が最も溶解度が低く、イオン性化合物が溶解度が高いことがわかります。A-2918は外れ値、つまり間違いなのでしょうか？また、NH\(_3\) は本当にこれらの有機化合物に匹敵するのでしょうか？このような疑問は、モデリングを行う前に検討すべきことです。

2.3.3. 特徴量の相関¶

次に、特徴量と溶解度(ラベル)の相関を調べてみましょう。 SD (標準偏差)、Ocurrences (その分子が構成するデータベースで何回出現したか)、Group (データの出所) など、特徴量や溶解度とは関係のないカラムがいくつかあることに注意してください。

features_start_at = list(soldata.columns).index("MolWt")
feature_names = soldata.columns[features_start_at:]

fig, axs = plt.subplots(nrows=5, ncols=4, sharey=True, figsize=(12, 8), dpi=300)
axs = axs.flatten()  # so we don't have to slice by row and column
for i, n in enumerate(feature_names):
    ax = axs[i]
    ax.scatter(
        soldata[n], soldata.Solubility, s=6, alpha=0.4, color=f"C{i}"
    )  # add some color
    if i % 4 == 0:
        ax.set_ylabel("Solubility")
    ax.set_xlabel(n)
# hide empty subplots
for i in range(len(feature_names), len(axs)):
    fig.delaxes(axs[i])
plt.tight_layout()
plt.show()

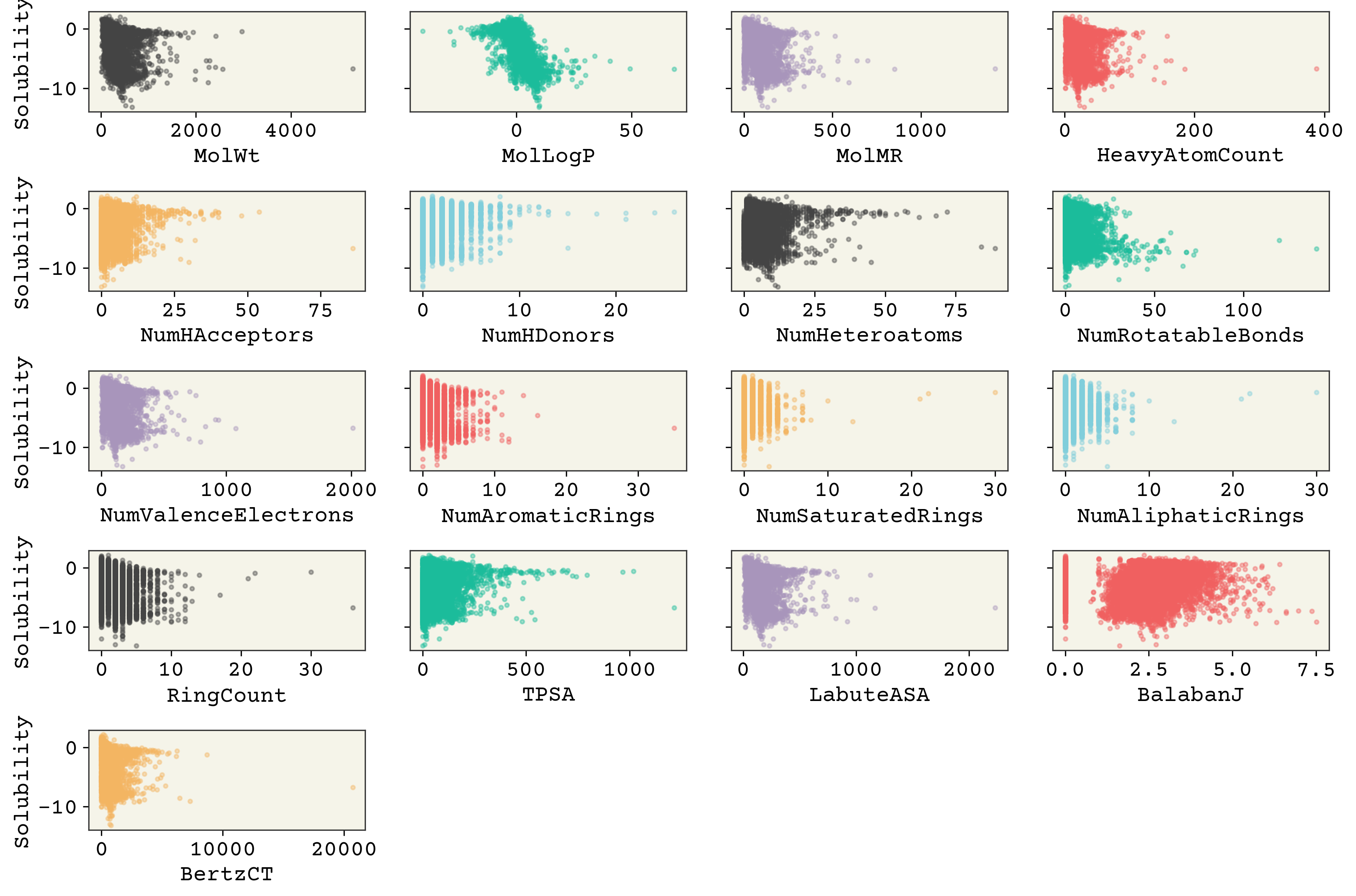
分子量や水素結合の数は、少なくともこのプロットからは、ほとんど相関がないように見えるのは興味深いことです。MolLogPは溶解性に関連する計算から導出された記述子で、よい相関を持っています。また、これらの特徴量のいくつかは、分散が低く、特徴の値が多くのデータに対してほとんど変化しないか、全く変化しないことがわかります（例えば、「NumHDonors」など）。

2.3.4. 線形モデル¶

まず、最も単純なアプローチの1つである線形モデルから始めましょう。これは教師あり学習の最初の例で、これから説明する特徴量の選択が難しいため、ほとんど使われることはありません。

この線形モデルは以下の方程式で定義されます。

(2.1)¶\[\begin{equation} y = \vec{w} \cdot \vec{x} + b \end{equation}\]

この式は1つのデータ点に対して定義されます。1つの特徴ベクトル \(\vec{x}\) の形状は、(17個の特徴があるため)今回の場合17です。\(\vec{w}\) は長さ17の調整可能なパラメータのベクトルで、 \(b\) は調整可能なスカラーです(バイアス と呼ばれます)。

このモデルは、jaxというライブラリを用いて実装します。このライブラリは、autodiffによって解析的勾配を簡単に計算できることを除けば、numpyに非常によく似ています。

def linear_model(x, w, b):
    return jnp.dot(x, w) + b


# test it out
x = np.array([1, 0, 2.5])
w = np.array([0.2, -0.5, 0.4])
b = 4.3

linear_model(x, w, b)

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

DeviceArray(5.5, dtype=float32)

ここで重要な問題が出てきます。 調整可能なパラメータ \(\vec{w}\) と \(b\) はどのように見つけるのでしょうか？ 線形回帰の古典的な方法では、 \(\vec{w} = (X^TX)^{-1}X^{T}\vec{y}\) という擬似逆行列を使って調整パラメータを直接計算します。詳しくはこちらに詳しく書いてあります。しかし、今回は、深層学習で行うことを考慮した反復的なアプローチを使用します。これは線形回帰の正しい計算方法ではありませんが、深層学習ではよく見る方法なので、反復的な計算方法に慣れるのに便利でしょう。

調整可能なパラメータを繰り返し見つけるために、損失関数を選び、勾配を用いて最小化することにします。これらの量を定義し、いくつかの初期値wとbを用いて損失を計算していきます。

# convert data into features, labels
features = soldata.loc[:, feature_names].values
labels = soldata.Solubility.values

feature_dim = features.shape[1]

# initialize our paramaters
w = np.random.normal(size=feature_dim)
b = 0.0

# define loss
def loss(y, labels):
    return jnp.mean((y - labels) ** 2)


# test it out
y = linear_model(features, w, b)
loss(y, labels)

DeviceArray(3265882.2, dtype=float32)

溶解度が-13から2であることを考えると、この損失はひどいものです。しかし、この結果はあくまで初期パラメータから予測しただけなので、この場合においては正しいのです。

2.3.5. 勾配降下法¶

ここで、調整可能なパラメータに対して損失がどのように変化するかという情報を使って、損失を減らしていきます。今回用いる損失関数を以下のように定義します。:

(2.2)¶\[\begin{equation} L = \frac{1}{N}\sum_i^N \left[y_i - f(\vec{x}_i, \vec{w}, b)\right]^2 \end{equation}\]

この損失関数は平均2乗誤差と呼ばれ、しばしばMSEと略されます。調整可能なパラメータに対する損失の勾配を計算することができます。

(2.3)¶\[\begin{equation} \frac{\partial L}{\partial w_i}, \frac{\partial L}{\partial b} \end{equation}\]

ここで、\(w_i\) は重みベクトル \(i\) 番目の要素である \(\vec{w}\) です。負の勾配の方向に微小量の変化を生むことで、損失を減らすことができます。:

(2.4)¶\[\begin{equation} (w_i, b') = \left(w_i - \eta \frac{\partial L}{\partial w_i}, b - \eta\frac{\partial L}{\partial b}\right) \end{equation}\]

ここで、 \(\eta\) は学習率であり、調整可能であるが、学習しないパラメータ（ハイパーパラメータと呼ばれます）です。この例では \(1\times10^{-6}\) と設定しています。一般的には10の累乗で表され、最大でも0.1程度になるように設定されます。それ以上の値は安定性に問題があることが知られています。それでは、gradient descentと呼ばれるこの手順を実装してみます。

# compute gradients
def loss_wrapper(w, b, data):
    features = data[0]
    labels = data[1]
    y = linear_model(features, w, b)
    return loss(y, labels)


loss_grad = jax.grad(loss_wrapper, (0, 1))

# test it out
loss_grad(w, b, (features, labels))

(DeviceArray([1.1313606e+06, 7.3055479e+03, 2.8128903e+05, 7.4776180e+04,
              1.5807716e+04, 4.1010732e+03, 2.2745816e+04, 1.7236283e+04,
              3.9615741e+05, 5.2891074e+03, 1.0585280e+03, 1.8357089e+03,
              7.1248174e+03, 2.7012794e+05, 4.6752903e+05, 5.4541211e+03,
              2.5596618e+06], dtype=float32),
 DeviceArray(2671.3784, dtype=float32, weak_type=True))

勾配の計算を行ったので、それを数ステップかけて最小化します。

loss_progress = []
eta = 1e-6
data = (features, labels)
for i in range(10):
    grad = loss_grad(w, b, data)
    w -= eta * grad[0]
    b -= eta * grad[1]
    loss_progress.append(loss_wrapper(w, b, data))
plt.plot(loss_progress)

plt.xlabel("Step")
plt.yscale("log")
plt.ylabel("Loss")
plt.title("Full Dataset Training Curve")
plt.show()

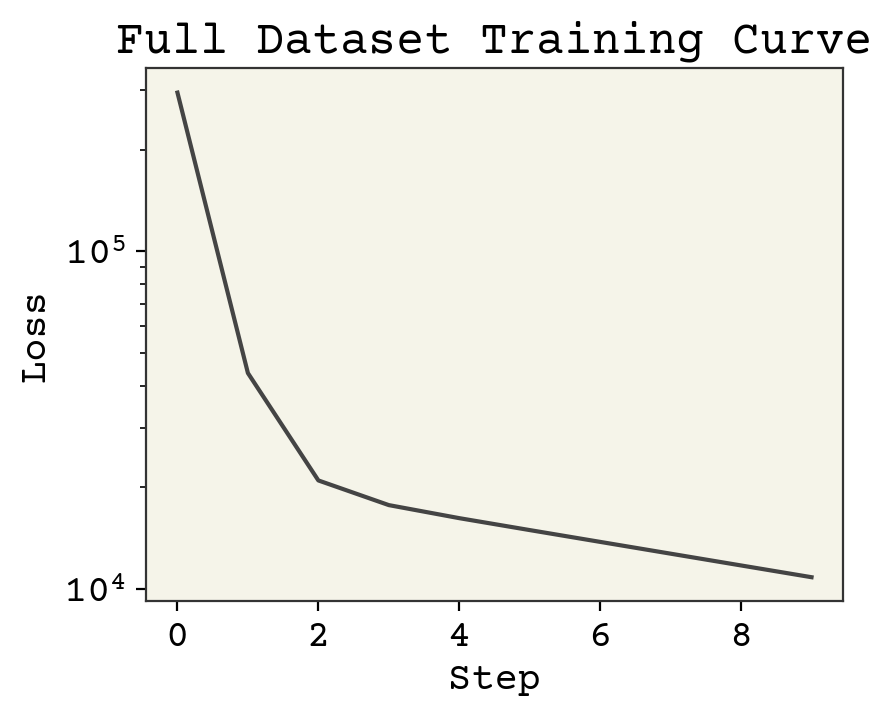
2.3.6. 学習曲線¶

上の図は 学習曲線 と呼ばれるものです。これは損失が減少しているかどうかを示しており、モデルが学習を行っていることを表しています。学習曲線は Learning Curve とも呼ばれます。X軸はサンプル数、データセットの総反復回数（エポックと呼ばれる）、モデルの学習に使用されたデータ量の他の指標が用いられます。

2.3.7. バッチ処理¶

勾配降下法によって学習が良い感じに進んでいることがわかります。しかし、ちょっとした変更で学習のスピードアップを図ることができます。機械学習で実際に行われている学習方法である バッチ処理 を使ってみましょう。ちょっとした変更点とは、すべてのデータを一度に使うのではなく、その部分集合の小さなバッチデータだけを取るということです。バッチ処理には2つの利点があります。1つはパラメータの更新を計算する時間を短縮できること、もう1つは学習過程をランダムにできることです。このランダム性により、学習の進行を止める可能性のあるる局所的な極小値から逃れることができます。このバッチ処理の追加により、この勾配降下法アルゴリズムは確率的となり、確率的勾配降下法（SGD）と呼ばれる手法になります。SGDとそのバリエーションは、深層学習における最も一般的な学習方法です。

# initialize our paramaters
# to be fair to previous method
w = np.random.normal(size=feature_dim)
b = 0.0

loss_progress = []
eta = 1e-6
batch_size = 32
N = len(labels)  # number of data points
data = (features, labels)
# compute how much data fits nicely into a batch
# and drop extra data
new_N = len(labels) // batch_size * batch_size

# the -1 means that numpy will compute
# what that dimension should be
batched_features = features[:new_N].reshape((-1, batch_size, feature_dim))
batched_labels = labels[:new_N].reshape((-1, batch_size))
# to make it random, we'll iterate over the batches randomly
indices = np.arange(new_N // batch_size)
np.random.shuffle(indices)
for i in indices:
    # choose a random set of
    # indices to slice our data
    grad = loss_grad(w, b, (batched_features[i], batched_labels[i]))
    w -= eta * grad[0]
    b -= eta * grad[1]
    # we still compute loss on whole dataset, but not every step
    if i % 10 == 0:
        loss_progress.append(loss_wrapper(w, b, data))

plt.plot(np.arange(len(loss_progress)) * 10, loss_progress)
plt.xlabel("Step")
plt.yscale("log")
plt.ylabel("Loss")
plt.title("Batched Loss Curve")
plt.show()

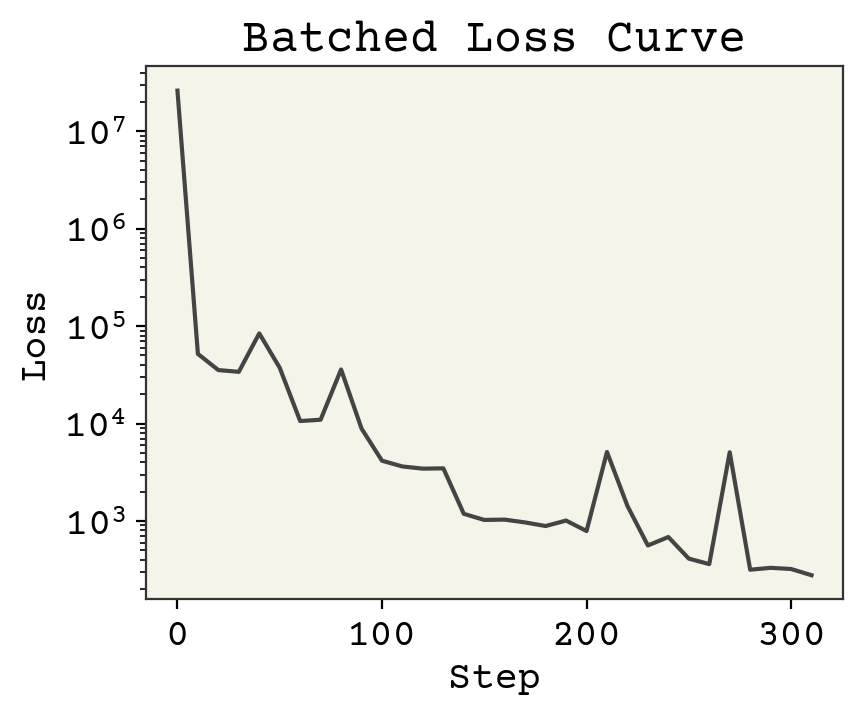
ここで注目すべき点は、以下の3つです。

バッチ処理を行わない場合に比べ、損失が小さくなっています。
データセットを10回で反復するのをやめ、1回だけ反復しているにも関わらず、ステップ数が増えています。
損失は常に減少するわけではありません。

損失が小さくなる理由は、各データポイントを1回しか見ていないにもかかわらず、より多くのステップを踏むことができるからです。バッチ処理を行うと、バッチごとに勾配降下法の更新を行うため、データセットに対して1回の反復でより多くの更新を行うことができます。具体的には \(B\) をバッチサイズとすると、元の勾配降下法では1回しか更新できない所、バッチ処理を行った場合は \(N / B\) 回の更新を行うことができます。損失が常に減少しない理由は、評価するたびに異なるデータセットであるためです。データセットからランダムに選定したバッチでは、ある分子が他の分子より予測が難しかったり、1つのバッチに基づいてパラメータを更新しただけなので、各ステップが正しく損失を最小化できているとは限らなかったりします。しかし、バッチがランダムに選定されていると仮定すれば、常に（平均的に）損失の減少量の期待値を向上させることができます。(つまり、損失の期待値を最小化できます)

2.3.8. 特徴量の標準化¶

損失関数の減少がある一定の値で止まっています。勾配を調べると、非常に大きいものもあれば、非常に小さいものもあることがわかります。ここで重要になってくるのは、それぞれの特徴は大きさが違うことです。例えば、学習で反映されるべきそれぞれの重要さとは無関係に、分子量は比較的大きな数字であり、分子の中の環の数は比較的小さな数字になります。これは学習に影響を与えており、それぞれは同じ学習率、 \(\eta\) を使わなければならないですが、その学習率が適切なものもあれば、小さすぎるものもあるという問題が発生しています。もし、 \(\eta\) を大きくすると、特徴量の勾配からウケる影響が大きくなるため、学習の速度が爆発的に増加してしまいます。そこで、統計の教科書に載っている標準化の式を用いて、全ての素性の大きさを同じにするのが標準的な解決策として取られています。

(2.5)¶\[\begin{equation} x_{ij} = \frac{x_{ij} - \bar{x_j}}{\sigma_{x_j}} \end{equation}\]

ここで、\(\bar{x_j}\) は列の平均、\(\sigma_{x_j}\) は列の標準偏差です。訓練データをテストデータで汚染しないように、つまり、訓練するときにテストデータの平均や標準偏差などの情報を使うことがないように、平均と標準偏差の計算には訓練データだけを使うようにします。テストデータは、未知のデータに対するモデルの性能を近似的に示すためのものであり、通常のタスクでは未知のデータがどのような特徴量を持つものであるかは分からないので、標準化のために学習時に使用することはできません。

fstd = np.std(features, axis=0)
fmean = np.mean(features, axis=0)
std_features = (features - fmean) / fstd

# initialize our paramaters
# since we're changing the features
w = np.random.normal(scale=0.1, size=feature_dim)
b = 0.0


loss_progress = []
eta = 1e-2
batch_size = 32
N = len(labels)  # number of data points
data = (std_features, labels)
# compute how much data fits nicely into a batch
# and drop extra data
new_N = len(labels) // batch_size * batch_size
num_epochs = 3

# the -1 means that numpy will compute
# what that dimension should be
batched_features = std_features[:new_N].reshape((-1, batch_size, feature_dim))
batched_labels = labels[:new_N].reshape((-1, batch_size))
indices = np.arange(new_N // batch_size)

# iterate through the dataset 3 times
for epoch in range(num_epochs):
    # to make it random, we'll iterate over the batches randomly
    np.random.shuffle(indices)
    for i in indices:
        # choose a random set of
        # indices to slice our data
        grad = loss_grad(w, b, (batched_features[i], batched_labels[i]))
        w -= eta * grad[0]
        b -= eta * grad[1]
        # we still compute loss on whole dataset, but not every step
        if i % 50 == 0:
            loss_progress.append(loss_wrapper(w, b, data))

plt.plot(np.arange(len(loss_progress)) * 50, loss_progress)
plt.xlabel("Step")
plt.yscale("log")
plt.ylabel("Loss")
plt.show()

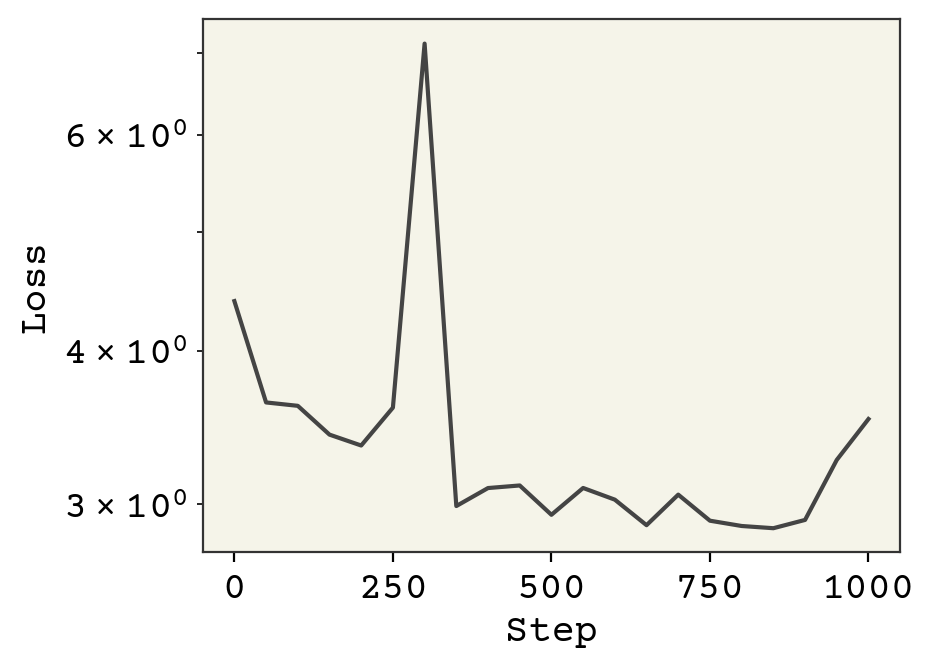
学習が不安定にならないまま、学習率を0.01まで上げることができました。これはすべての特徴が同じオーダーになったことにより可能となっています。また、これらのモデルの改良により、更なる学習を続けることも可能になります。

2.3.9. モデル性能の分析¶

これは重要な事柄なので、後で詳しく調べますが，教師あり学習で通常最初に調べるのはパリティプロットで，予測値とラベル予測値を用いた図を作ります．このプロットの良いところは、特徴量の次元に関係なく機能することです。モデルが完全に機能している場合、すべてのデータは \(y = \hat{y}\) 上にプロットされます。

predicted_labels = linear_model(std_features, w, b)

plt.plot([-100, 100], [-100, 100])
plt.scatter(labels, predicted_labels, s=4, alpha=0.7)
plt.xlabel("Measured Solubility $y$")
plt.ylabel("Predicted Solubility $\hat{y}$")
plt.xlim(-13.5, 2)
plt.ylim(-13.5, 2)
plt.show()

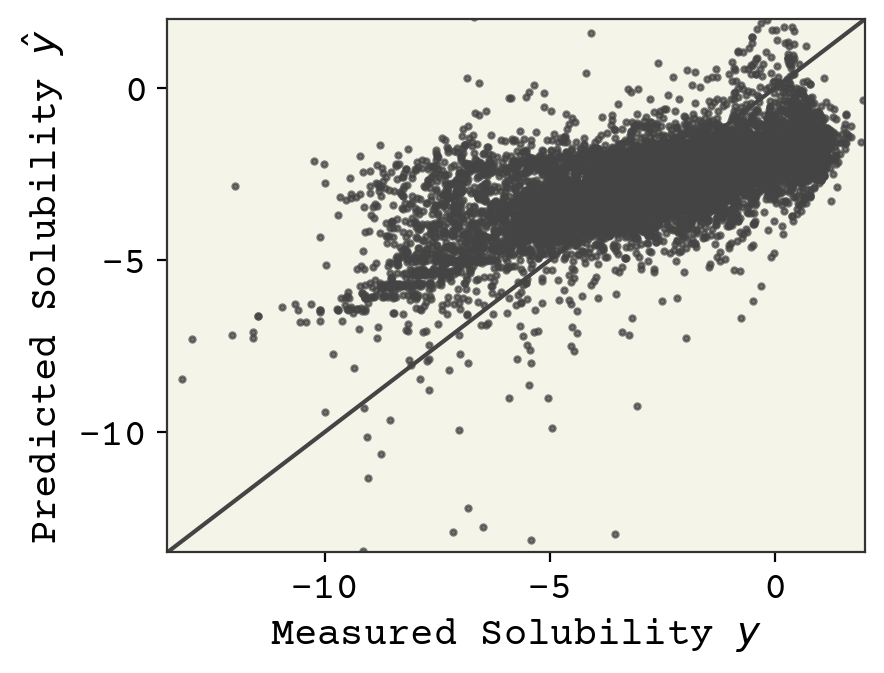
最終的なモデルの評価は損失の値で行うことができますが、通常、他の指標も使用されます。回帰分析では、損失に加えて相関係数が計算されることが多いです。相関係数は次のように計算されます。

# slice correlation between predict/labels
# from correlation matrix
np.corrcoef(labels, predicted_labels)[0, 1]

0.6475304402750964

0.65は相関係数として悪くはないですが、素晴らしいとは言えません。

2.4. 教師なし学習¶

教師なし学習では、ラベルがない状態で \(\hat{y}\)を予測することが目標です。これは不可能なことのように思えますが、どのように成功を判断するのでしょうか。一般に、教師なし学習は3つのカテゴリに分けられます。

クラスタリング

このカテゴリでは、 \(\{y_i\}\) をクラス変数と仮定し、特徴をクラスに分割することを試みます。クラスタリングでは、クラスの定義（クラスタと呼ばれます）と各特徴量がどのクラスタに割り当てられるべきかを同時に学習することになります。

シグナルのデノイジング

このタスクでは、\(x\) はノイズとシグナル（\(y\)）の2つの成分からできていると仮定し、シグナルの\(y\)を\(x\)から抽出し、ノイズを除去することを目標とします。後述する表現学習と高い関連性を持ちます。

生成的モデル

生成的モデルは、 \(P(\vec{x})\) を学習して、\(\vec{x}\) の新しい値をサンプリングする方法です。これは、\(y\)を確率とし、それを推定しようとすることに似ています。これらについては、後で詳しく説明します。

2.4.1. クラスタリング¶

クラスタリングは歴史的に最もよく知られた機械学習手法の1つであり，今でも良く用いられています。クラスタリングは何もないところにクラスラベルを与えるので、データ中のパターンを見つけ、データから新しい洞察を得るのに役立ちます。そして、化学（そしてほとんどの分野）であまり人気がなくなった理由でもありますが、クラスタリングには正解も不正解もありません。クラスタリングは、二人の人間が独立して行うと、しばしば異なる答えに到達します。とはいえ、クラスタリングは知っておくべきツールであり、良い探索戦略にもなり得ます。

ここでは、古典的なクラスタリング手法であるk-meansについて見ていきます。Wikipediaにこの古典的なアルゴリズムに関するすばらしい記事があるので、その内容について繰り返すのはやめておきます。クラスタリングの結果を実際に見えるようにするために、特徴量を2次元に投影することから始めます。これは表現学習で詳細に説明されるので、これらのステップについての理解を心配する必要はありません。(訳注: 本当か？)

# get down to 2 dimensions for easy visuals
embedding = sklearn.manifold.Isomap(n_components=2)
# only fit to every 25th point to make it fast
embedding.fit(std_features[::25, :])
reduced_features = embedding.transform(std_features)

極端に離れている外れ値もあるので（それはそれで面白いのですが）、データの真ん中99パーセンタイルについて注目していきます。

xlow, xhi = np.quantile(reduced_features, [0.005, 0.995], axis=0)

plt.figure(dpi=300)
plt.scatter(
    reduced_features[:, 0],
    reduced_features[:, 1],
    s=4,
    alpha=0.7,
    c=labels,
    edgecolors="none",
)
plt.xlim(xlow[0], xhi[0])
plt.ylim(xlow[1], xhi[1])
cb = plt.colorbar()
cb.set_label("Solubility")
plt.show()

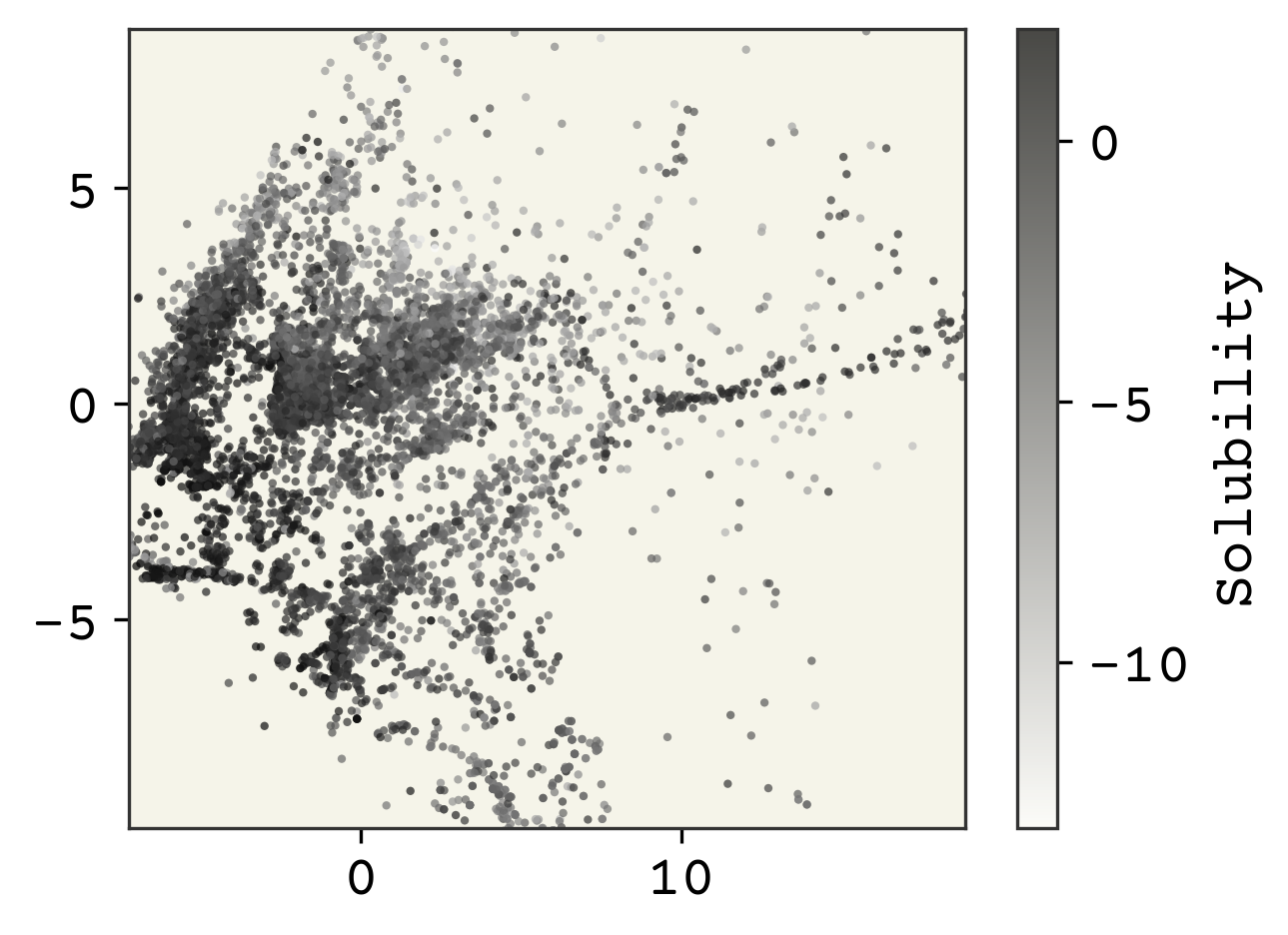
次元削減により、特徴量ははわずか2次元となりました。溶解度のクラスによって色を付けることで、いくつかの構造を見ることができます。このような次元削減を行った結果のプロットでは、軸は任意であるため、ラベルを付けないことに注意してください。

続けて、クラスタリングを行います。クラスタリングの主な課題は、クラスタをいくつにするか決めることです。いろいろな方法がありますが、基本的には直感に頼ることになります。つまり、化学者として、データ以外の何らかのドメイン知識を使って、クラスタ数を直感的に決める必要があります。非科学的に聞こえますか？だからクラスタリングは難しいんです。

# cluster - using whole features
kmeans = sklearn.cluster.KMeans(n_clusters=4, random_state=0)
kmeans.fit(std_features)

とても簡単な手順ですね。では、データを割り当てられたクラスで色付けして可視化してみます。

plt.figure(dpi=300)
point_colors = [f"C{i}" for i in kmeans.labels_]
plt.scatter(
    reduced_features[:, 0],
    reduced_features[:, 1],
    s=4,
    alpha=0.7,
    c=point_colors,
    edgecolors="none",
)
# make legend
legend_elements = [
    plt.matplotlib.patches.Patch(
        facecolor=f"C{i}", edgecolor="none", label=f"Class {i}"
    )
    for i in range(4)
]
plt.legend(handles=legend_elements)
plt.xlim(xlow[0], xhi[0])
plt.ylim(xlow[1], xhi[1])
plt.show()

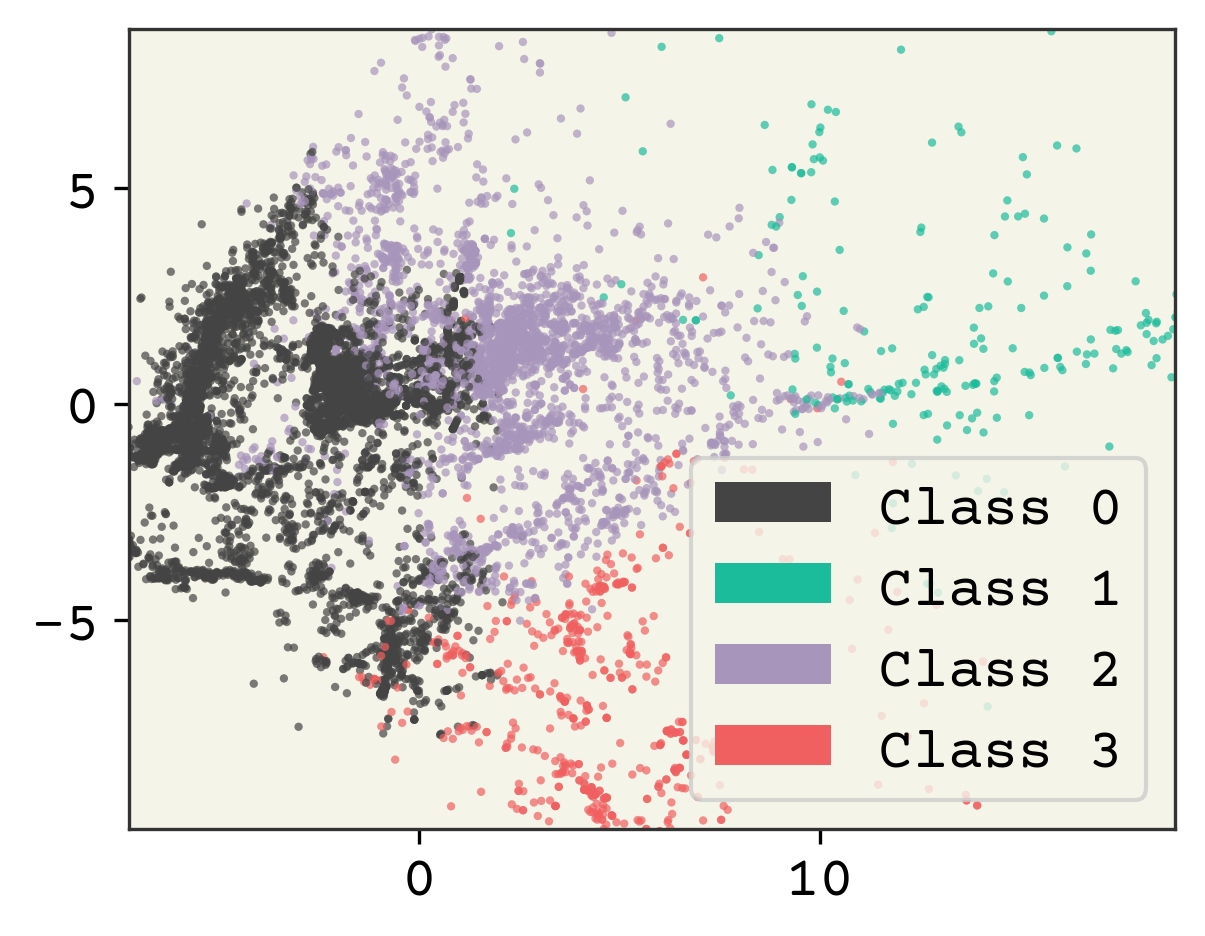
2.4.2. クラスター数の選択¶

どうやってクラスターの数を正しく決められたかを判断するのでしょうか？答えは直感です。エルボープロットと呼ばれる、学習曲線のように使うことのできるツールがあります。k-meansのクラスタは、クラスタ中心からの平均二乗距離を計算することで損失関数として使うことができます。しかし、クラスタ数を学習可能なパラメータとして扱うと、クラスタ数とデータ点数が等しい(つまり、1つのクラスタに1つのデータが入る)ときに最もフィットすることがわかります。これでは意味がありません。しかし、この損失関数の傾きがほぼ一定になる点が存在し、クラスタを追加することで新しい見識を追加していないと判定することができます。損失をプロットして何が起こるか見てみましょう。時間を節約するために、データセットのうち一部のサンプルを使用していることに気を付けてください。バッチ処理と同じような考え方です。

# make an elbow plot
loss = []
cn = range(2, 15)
for i in cn:
    kmeans = sklearn.cluster.KMeans(n_clusters=i, random_state=0)
    # use every 50th point
    kmeans.fit(std_features[::50])
    # we get score -> opposite of loss
    # so take -
    loss.append(-kmeans.score(std_features[::50]))

plt.plot(cn, loss, "o-")
plt.xlabel("Cluster Number")
plt.ylabel("Loss")
plt.title("Elbow Plot")
plt.show()

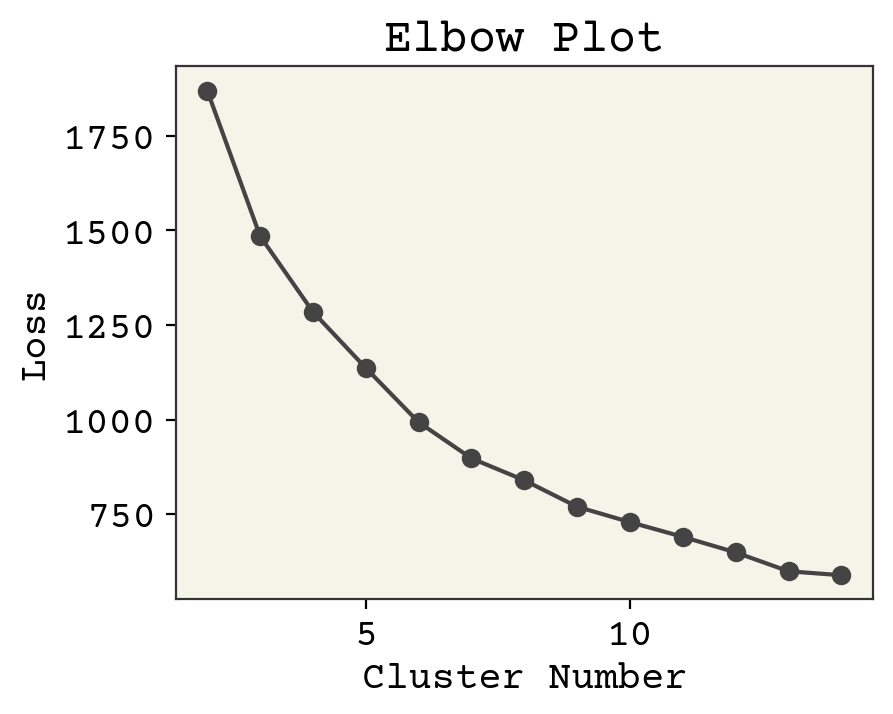
変わり目はどこでしょうか？よくよく見てみると、たぶん、6? 3? 4? 7? 今回は4を選びましょう。響きがいいし、データに基づくともっともらしいからです。最後の作業は、クラスタが実際に何であるかを知ることです。最も中心にあるデータポイント（つまり、クラスタの中心に最も近いデータ）を抽出し、それらをクラスタの代表とみなします。

# cluster - using whole features
kmeans = sklearn.cluster.KMeans(n_clusters=4, random_state=0)
kmeans.fit(std_features)

cluster_center_idx = []
for c in kmeans.cluster_centers_:
    # find point closest
    i = np.argmin(np.sum((std_features - c) ** 2, axis=1))
    cluster_center_idx.append(i)
cluster_centers = soldata.iloc[cluster_center_idx, :]

legend_text = [f"Class {i}" for i in range(4)]

# now plot them on a grid
cluster_mols = [rdkit.Chem.MolFromInchi(inchi) for inchi in cluster_centers.InChI]
rdkit.Chem.Draw.MolsToGridImage(
    cluster_mols, molsPerRow=2, subImgSize=(400, 400), legends=legend_text
)

では、これらのクラスは一体何なのでしょうか？不明です。意図的に溶解度を明らかにしなかった（教師なし学習）ので、必ずしも溶解度と関係があるわけではありません。これらのクラスは、むしろデータセットにどのような特徴が選ばれたかの結果です。クラス1はすべて負電荷であるとか、クラス0は脂肪族であるといった仮説を立てて、検討することができます。しかし、ベストなクラスタリングを選ぶことはできませんし、教師なし学習は洞察やパターンを見つけることが重要で、精度の高いモデルを作ることが重要なのではありません。

エルボープロット法は、クラスタ番号を選択するための多くのアプローチの1つです [PDN05]. 私は、直感を利用していることが明確なので、この方法を好んでいます。より洗練された方法は、クラスタリングに正解も不正解もないという事実をある種隠蔽しています。

Note

このプロセスでは、溶解度を予測する関数は得られません。予測されたクラスで溶解度の予測に関する見識を得られるかもしれませんが、それはクラスタリングの目的ではありません。

2.5. まとめ¶

教師あり機械学習とは、入力の特徴量 \(\vec{x}\) からラベル \(y\) を予測するモデルを構築することです。
データはラベル付きでもラベルなしでも適用可能です。
確率的勾配降下法を用いて、損失を最小化することでモデルを学習できます。
教師なし学習とは、データのパターンを発見するモデルを作ることです。
クラスタリングは教師なし学習の1つであり、モデルがデータ点をクラスタに分けます。

2.6. 練習問題¶

2.6.1. データ処理¶

numpyの np.amin, np.std などを使って（pandas ではありません！）、すべてのデータ点についての各特徴の平均、最小、最大、標準偏差を計算してください。
rdkit を使って、分子量の大きい2つの分子を描いてください。また、その構造の変な点を挙げてください。

2.6.2. 線形モデル¶

\(y = \vec{w_1} \cdot \sin\left(\vec{x}\right) + \vec{w_2} \cdot \vec{x} + b\) のような非線形モデルが線形モデルで表現できることを証明してください。
線形モデル方程式をアインシュタインの縮約記法でバッチ式に書き出しなさい。バッチ形式とは、バッチを示すインデックスを明示的に持つことである。例えば、ラベルは\(y_{bi}\)となり、\(b\)はデータのバッチを、\(i\)は個々のデータ点を示す。

2.6.3. 損失関数の最小化¶

今回のnotebookでは、特徴量は標準化したが、ラベルは標準化しませんでした。ラベルを標準化することは、学習率の選択に影響を与えるか？説明してください。
平均二乗誤差ではなく、平均絶対誤差の損失を実装してください。その勾配を jax を使って計算してください。
標準化された特徴量を用いて、バッチサイズが学習にどのような影響を与えるかを示してください。バッチサイズは1、8、32、256、1024を使用してください。各実行の間に重みを初期化しなければならないことに注意してください。そして、各バッチサイズでのlog-lossを同じプロット上にプロットし、その結果を説明してください。

2.6.4. クラスタリング¶

クラスタリングは教師なし学習の一種であり、ラベルを予測すると述べました。クラスタリングで予測されるラベルとは、具体的にどのようなものでしょうか。いくつかのデータポイントについて、予測されるラベルがどのようなものか書き出してみてください。
クラスタリングでは、特徴量からラベルを予測します。ラベルがあっても、それを特徴量と見なしてクラスタリングすることができます。このように、ラベルを特徴量として扱い、クラスを表す新しいラベルを予測しようとするクラスタリングが良くない理由を2つ述べてください。
Isomapプロット（縮小次元プロット）上で、点がどのグループに属するか（G1、G2など）で色分けしてください。これとクラスタリングの間に何か関係があるでしょうか。

2.7. Cited References¶

Alp20: Ethem Alpaydin. Introduction to machine learning. MIT press, 2020.
FZJS21: Victor Fung, Jiaxin Zhang, Eric Juarez, and Bobby G. Sumpter. Benchmarking graph neural networks for materials chemistry. npj Computational Materials, June 2021. URL: https://doi.org/10.1038/s41524-021-00554-0, doi:10.1038/s41524-021-00554-0.
Bal19: Prasanna V Balachandran. Machine learning guided design of functional materials with targeted properties. Computational Materials Science, 164:82–90, 2019.
GomezBAG20: Rafael Gómez-Bombarelli and Alán Aspuru-Guzik. Machine learning and big-data in computational chemistry. Handbook of Materials Modeling: Methods: Theory and Modeling, pages 1939–1962, 2020.
NDJ+18: Aditya Nandy, Chenru Duan, Jon Paul Janet, Stefan Gugler, and Heather J Kulik. Strategies and software for machine learning accelerated discovery in transition metal chemistry. Industrial & Engineering Chemistry Research, 57(42):13973–13986, 2018.
Wei88: David Weininger. Smiles, a chemical language and information system. 1. introduction to methodology and encoding rules. Journal of chemical information and computer sciences, 28(1):31–36, 1988.
SKE19: Murat Cihan Sorkun, Abhishek Khetan, and Süleyman Er. AqSolDB, a curated reference set of aqueous solubility and 2D descriptors for a diverse set of compounds. Sci. Data, 6(1):143, 2019. doi:10.1038/s41597-019-0151-1.
PDN05: Duc Truong Pham, Stefan S Dimov, and Chi D Nguyen. Selection of k in k-means clustering. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 219(1):103–119, 2005.

1. Tensors and Shapes

3. Regression & Model Assessment

deep learning for molecules & materials