Graph Neural Networks

8. Graph Neural Networks¶

歴史的に、機械学習で分子を扱う際の最大の課題は、記述子の選定とその計算でした。グラフニューラルネットワーク（GNN）は、グラフを入力とするディープニューラルネットワークの一種であり、GNNは分子を直接入力として受け取ることができるため、記述子に頭を悩ませる必要がありません。

本章の想定読者と目的

この章では、Standard Layers と Regression & Model Assessment の内容は前提としています。本章ではグラフやGNNの定義から説明しますが、グラフやニューラルネットワークの基本的な概念について予め慣れているとなお良いでしょう。この章を学ぶことで、以下ができるようになります：

分子をグラフで表現できる
一般的なGNNのアーキテクチャを議論したり、GNNの種類を理解できる
GNNを構築し、ラベルの種類に応じた読み出し関数（read-out function）を選択できる
グラフ、エッジ、ノードの特徴をそれぞれ区別できる
GNNをエッジ更新、ノード更新、集約の各ステップに分けて定式化できる

GNNはグラフを入力および出力するために特別に設計されたレイヤーです。GNNについてのレビューは複数執筆されており、例えば Dwivedi et al.[DJL+20], Bronstein et al.[BBL+17], Wu et al.[WPC+20] などが挙げられます。 GNNは、粗視化分子動力学シミュレーション [LWC+20] からNMRの化学シフト予測 [YCW20] 、固体のダイナミクスのモデリング [XFLW+19] まで、あらゆるアプリケーションに適用できます。 GNNについて深く踏み込む前に、まずグラフがコンピュータ上でどのように表現され、分子がどのようにグラフに変換されるか理解しましょう。

グラフとGNNについてのインタラクティブな入門資料が、 distill.pub [SLRPW21] で提供されています。現在のGNNの研究のほとんどは、グラフに特化したディープラーニングライブラリを用いて行われており、2022年現在最も代表的なライブラリは PyTorch Geometric, Deep Graph library, Spektral, TensorFlow GNNS などです。

8.1. グラフの表現¶

グラフ \(\mathbf{G}\) は、ノード \(\mathbf{V}\) およびエッジ \(\mathbf{E}\)　の集合です。我々のセッティングでは、ノード \(i\) はベクトル \(\vec{v}_i\) で定義されるので、ノードの集合はランク2のテンソルとして表現できます。エッジは隣接行列（adjacency matrix） \(\mathbf{E}\) で表現され、もし \(e_{ij} = 1\) であればノード \(i\) と \(j\) がエッジで結合しているとみなされます。グラフを扱う多くの分野において、簡単のため、グラフはしばしば有向非巡回グラフ（エッジには向きがあるが、一周して元のノードには戻らない）であると仮定されます。しかし、分子において結合には向きが無く、輪を持つ（巡回する）場合もあることに注意してください。化学結合において向きの概念はないことから、我々が扱う隣接行列は常に対称（\(e_{ij} = e_{ji}\)）となります。また、しばしばエッジ自身も特徴を持つ場合があり、 \(e_{ij}\) 自体をベクトルとすることで表現します。この場合は隣接行列はランク3のテンソルとなります。エッジ特徴の例としては、共有結合の次数や、2つのノード間の距離（＝原子間距離）などが挙げられます。

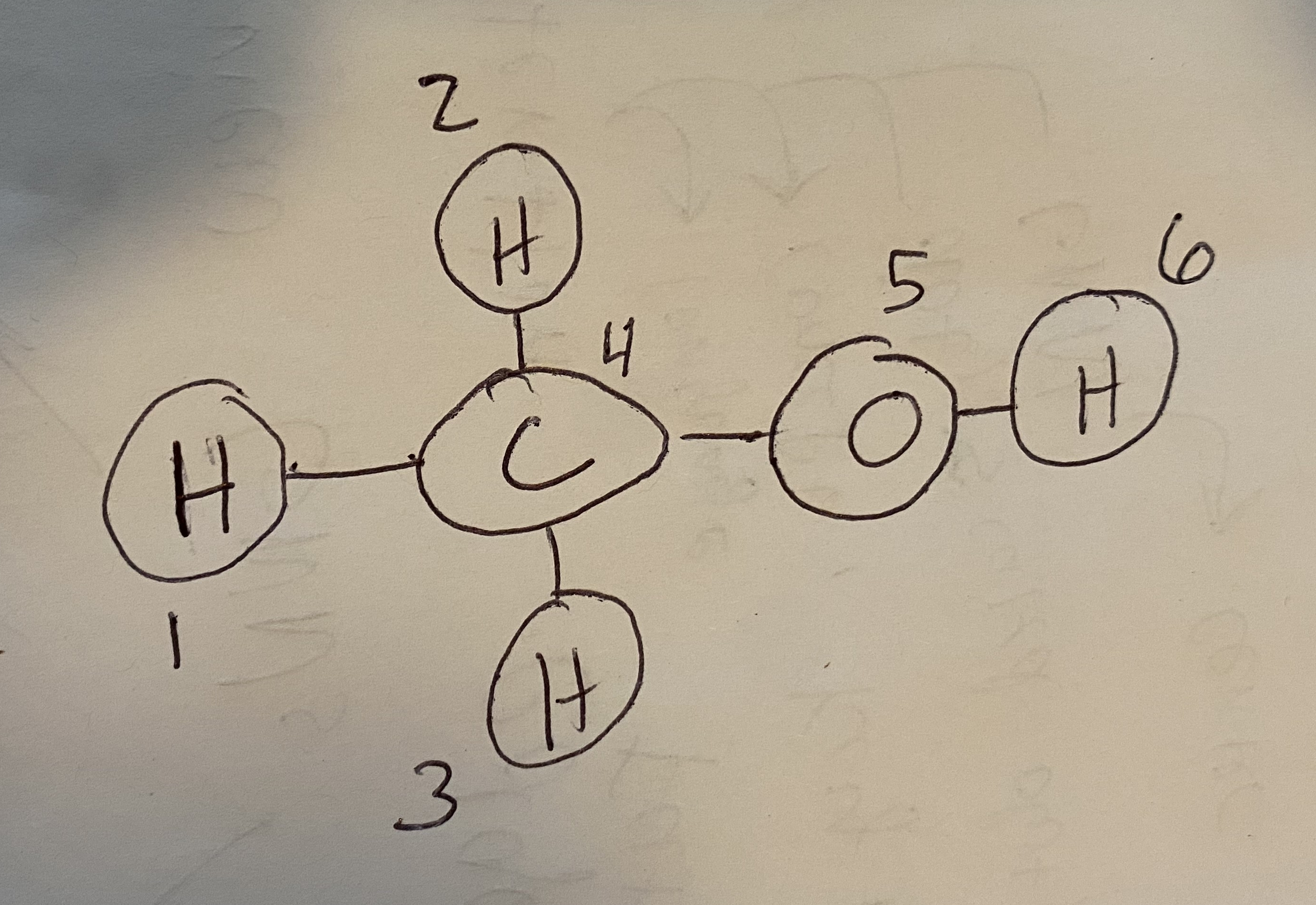
../_images/methanol.jpg — Fig. 8.1 グラフに変換できるよう、メタノールの各原子に番号を割り当てた¶

では、分子からどのようにグラフを構築できるか見てみましょう。例として、メタノールを考えます（ Fig. 8.1 ）。ノードとエッジを定義するため、便宜的に各原子に番号を振りました。まずはじめはノード特徴を考えます。ノードの特徴量には何を使っても良いのですが、多くの場合、one-hotエンコーディングされた特徴ベクトルを使うことになるでしょう：

Node	C	H	O
1	0	1	0
2	0	1	0
3	0	1	0
4	1	0	0
5	0	0	1
6	0	1	0

\(\mathbf{V}\) が、これらのノードについての結合された特徴ベクトルになります。このグラフの近接行列 \(\mathbf{E}\) は次のようになるでしょう：

	1	2	3	4	5	6
1	0	0	0	1	0	0
2	0	0	0	1	0	0
3	0	0	0	1	0	0
4	1	1	1	0	1	0
5	0	0	0	1	0	1
6	0	0	0	0	1	0

多少時間をかけてもよいので、これら2つをしっかりと理解してください。例えば、1,2,3行目については、4列目の成分だけが0でないことに注目してください。これは、原子1〜3は炭素（原子4）にのみ結合しているからです。また、原子は自分自身とは結合できないので、対角成分は常に0になります。

分子だけでなく、結晶構造についても似た方法でグラフ化できます。これについては Xie et al.による [XG18] を参照してください。

それでは、SMILESによる分子の文字列表現をグラフに変換する関数を定義するところから始めましょう。

8.2. このノートブックの動かし方¶

このページ上部のを押すと、このノートブックがGoogle Colab.で開かれます。必要なパッケージのインストール方法については以下を参照してください。

Tip

必要なパッケージをインストールするには、新規セルを作成して次のコードを実行してください。

!pip install dmol-book

もしインストールがうまくいかない場合、パッケージのバージョン不一致が原因である可能性があります。動作確認がとれた最新バージョンの一覧はここから参照できます

import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
import tensorflow as tf
import pandas as pd
import rdkit, rdkit.Chem, rdkit.Chem.rdDepictor, rdkit.Chem.Draw
import networkx as nx
import dmol

soldata = pd.read_csv(
    "https://github.com/whitead/dmol-book/raw/master/data/curated-solubility-dataset.csv"
)
np.random.seed(0)
my_elements = {6: "C", 8: "O", 1: "H"}

下の非表示セルでは、関数 smiles2graph を定義しています。この関数は元素C, H, Oについてone-hotなノード特徴ベクトルを生成します。また同時に、このone-hotベクトルを特徴ベクトルとする隣接テンソルを生成します。

def smiles2graph(sml):
    """Argument for the RD2NX function should be a valid SMILES sequence
    returns: the graph
    """
    m = rdkit.Chem.MolFromSmiles(sml)
    m = rdkit.Chem.AddHs(m)
    order_string = {
        rdkit.Chem.rdchem.BondType.SINGLE: 1,
        rdkit.Chem.rdchem.BondType.DOUBLE: 2,
        rdkit.Chem.rdchem.BondType.TRIPLE: 3,
        rdkit.Chem.rdchem.BondType.AROMATIC: 4,
    }
    N = len(list(m.GetAtoms()))
    nodes = np.zeros((N, len(my_elements)))
    lookup = list(my_elements.keys())
    for i in m.GetAtoms():
        nodes[i.GetIdx(), lookup.index(i.GetAtomicNum())] = 1

    adj = np.zeros((N, N, 5))
    for j in m.GetBonds():
        u = min(j.GetBeginAtomIdx(), j.GetEndAtomIdx())
        v = max(j.GetBeginAtomIdx(), j.GetEndAtomIdx())
        order = j.GetBondType()
        if order in order_string:
            order = order_string[order]
        else:
            raise Warning("Ignoring bond order" + order)
        adj[u, v, order] = 1
        adj[v, u, order] = 1
    return nodes, adj

nodes, adj = smiles2graph("CO")
nodes

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.],
       [0., 0., 1.],
       [0., 0., 1.],
       [0., 0., 1.]])

8.3. グラフニューラルネットワーク¶

グラフニューラルネットワーク (GNN) は、次の2つの特徴を持つニューラルネットワークです。

入力がグラフである
出力は順序等価（permutation equivariant）である

最初の点は明らかですが、2つめの特徴は説明が必要でしょう。まず、グラフの並べ替えとは、ノードを並べ替えることを意味します。上のメタノールの例では、炭素を原子4ではなく原子1にすることも簡単にできます。その場合、新しい隣接行列は次のようになります：

	1	2	3	4	5	6
1	0	1	1	1	1	0
2	1	0	0	0	0	0
3	1	0	0	0	0	0
4	1	0	0	0	1	0
5	1	0	0	0	0	1
6	0	0	0	0	1	0

この隣接行列の交換に正しく対応してGNNの出力が変換するなら、そのGNNは順序等価であると言えます。部分電荷や化学シフトのように原子ごとに定義される量をモデリングする場合、このような順序不変の仕組みは不可欠です。つまり、もし原子を入力する順序を変えれば、予測される部分電荷の順序も同様に変わってほしいのです。

もちろん、溶解度やエネルギーのように分子全体の特性をモデリングしたい場合もあります。これらの量は原子の順番を変えても 不変（invariant） であるべきです。順序について等価（equivariant）なモデルを不変（invariant）にするため、後に定義するリードアウト（read-out）を使います。等価性についてのより詳細な議論は Input Data & Equivariances を参照してください。

8.3.1. シンプルなGNN¶

我々はこれからGNNに言及しますが、実際にはGNN全体ではなく特定のレイヤーのことを指します。多くのGNNはグラフを取り扱うために特別に設計されたレイヤーを備えており、通常はこのレイヤーについてのみ関心を持ちます。それでは、GNNの簡単なレイヤーの例を見てみましょう:

(8.1)¶\[\begin{equation} f_k = \sigma\left( \sum_i \sum_j v_{ij}w_{jk} \right) \end{equation}\]

この式は、まず各ノード（\(v_{jij}\)）の特徴に学習可能な重み \(w_{jk}\) をかけた後、全てのノードの特徴を合計し、活性化を適用することを表しています。この操作により、グラフに対して1つの特徴ベクトルが得られます。では、この式は順序等価でしょうか？答えはYesです。なぜならこの式においてノードインデックスはインデックス \(i\) であり、出力に影響を与えることなく順序の並べ替えが可能であるためです。

では次に、この例と似ているが順序等価ではない例を見てみましょう。

(8.2)¶\[\begin{equation} f_k = \sigma\left( \sum_i v_{ij}w_{ik} \right) \end{equation}\]

これは小さな変化です。いま、ノードごとに1つの重みベクトルがあります。したがって、学習可能な重みはノードの順序に依存します。次に、ノードの順序を入れ替えると、学習した重みはノードに対応しなくなります。よって、ノード（＝原子）の順番を変えた2つのメタノール分子を入力すると、異なる出力が得られます。実際のところ、この単純な例は2つの点で実際のGNNと異なります。1つめは単一の特徴ベクトルを出力してノードごとの情報を捨ててしまっている点、2つめは隣接行列を使用しない点です。では、順序等価を維持し、かつこれら2つの性質を備えた実際のGNNを見てみましょう。

8.4. Kipf & Welling GCN¶

初期に人気があったGNNの一つは、Kipf & Welling graph convolutional network (GCN) [KW16] です。GCNをGNNの広いクラスの一つとして考える人もいますが、本書でGCNとは特にKipf & Welling GCNを指すものとします。 Thomas Kipfは、GCNの優れた紹介記事を書いています。

GCNレイヤーへの入力はノードおよびエッジの集合（訳注：各ノードおよびエッジはベクトルで表現されるので、これらの集合はテンソルです） \(\mathbf{V}\), \(\mathbf{E}\) で、出力は更新されたノードの集合 \(\mathbf{V}'\) です。各ノード特徴の更新は、 \(\mathbf{E}\) により表現される近傍ノードの特徴ベクトルを平均することでなされます。

近傍ノードの情報を平均することで、GCNレイヤーはノードについて順序等価になっています。近傍について平均するという操作そのものは学習できないので、特徴ベクトルを加算してからノードの次数（結合している近傍ノード数）で除算することで計算します。平均をとる前に、学習可能な重み行列を近傍特徴に掛けることにします。これによりGCNがデータから学習することが可能になります（訳注：言い換えれば、GCNの学習とはこの重み行列の要素を最適化することです）。この操作は次のように記述されます：

(8.3)¶\[ v_{il} = \sigma\left(\frac{1}{d_i}e_{ij}v_{jk}w_{lk}\right) \]

\(i\) は着目しているノード、 \(j\) はその近傍インデックス, \(k\) はノードの入力特徴、 \(l\) はノードの出力特徴、 \(d_i\) はノードの次数（次数で割ることで単なる加算ではなく平均になります）、 \(e_{ij}\) は、全ての非近傍ノードが \(v_{jk}\) ゼロになるよう近傍と非近傍ノードを分離する項、 \(\sigma\) は活性化関数、 \(w_{lk}\) は学習可能な重みです。この式はとても長いように見えますが、実際にやっていることは、近傍同士の平均に学習可能な重み行列を追加しただけです。この式のよくある拡張として、各ノードの近傍として自分自身も加える場合があります。これはノードの出力特徴 \(v_{il}\) が入力特徴 \(v_{ik}\) に依存するようにするためです。しかし、我々はこのために上の式を修正する必要はありません。もっとシンプルなやり方として、データの前処理で恒等行列を加算し、近接行列の対角成分を \(0\) ではなく\(1\) にしてやればよいのです。

GCNについての理解を深めることは、他の種類のGNNを理解するために重要です。ここでは2つのポイントを押さえてください。まずGCNレイヤーは、ノードとその近傍の間で”通信”する方法と見ることができます。ノード \(i\) についての出力は、そのすぐ隣のノードにのみ依存することになりますが、化学の場合、これでは不十分です。より遠方のノードの情報を取り込むために、我々は複数のGCNレイヤーを重ねることができます。もし2つのGCNレイヤーがあれば、ノード \(i\) の出力は、その隣の隣のノードの情報も含むことになります。 GCNで理解すべきもう一つの点は、ノード特徴を平均化するステップが2つの目的を達していることです：i)近傍ノードの順序を無視することで順序に対して等価となる、ii)ノード特徴のデータのスケール変化を防ぐ。単にノード特徴の和を取った場合、(i)は実現しますが、各レイヤーを通すごとにノード特徴のデータの値が大きくなってしまいます。もちろん、特徴のスケールを揃えるために各GCNレイヤーの後でバッチ平均化（batch normalization）レイヤーを通すという対処もありますが、平均化はよりシンプルです。

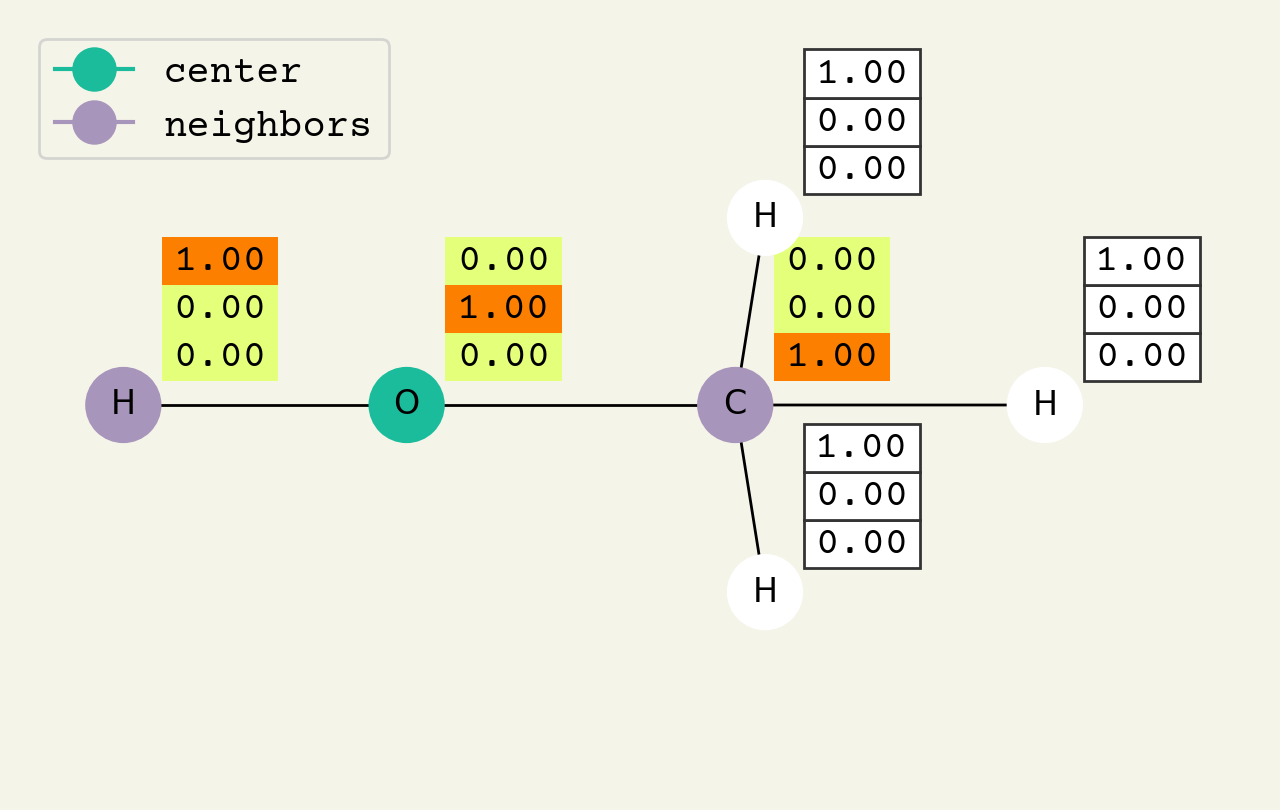
../_images/gnn_11_0.png — Fig. 8.2 グラフ畳み込みレイヤーの中間ステップ。3次元ベクトルはノード特徴であり、初期値は水素を表すone-hotベクトル `[1.00, 0.00, 0.00]` です。この中心ノードは、隣接するノードの特徴を平均することで更新されていきます。¶

GCNレイヤーを理解しやすくするため、 Fig. 8.2 を見てください。これはGCNレイヤーの中間ステップを表しています。各ノードの特徴は、ここではone-hot encodingされたベクトルとして表現されています。Fig. 8.3 のアニメーションは、近傍特徴についての平均化プロセスを表しています。このアニメーションでは、わかりやすくするために学習可能な重みと活性化関数は記述されていません。このアニメーションは2層目のGCNレイヤーでも繰り返されることに注意してください。分子中に酸素原子が含まれるという”情報”が、2層目ではじめて各原子に伝搬される様子をよく見てください。全てのGNNは似たようなアプローチで動作するので、このアニメーションの内容はとても大切です。ぜひ、よく理解してください。

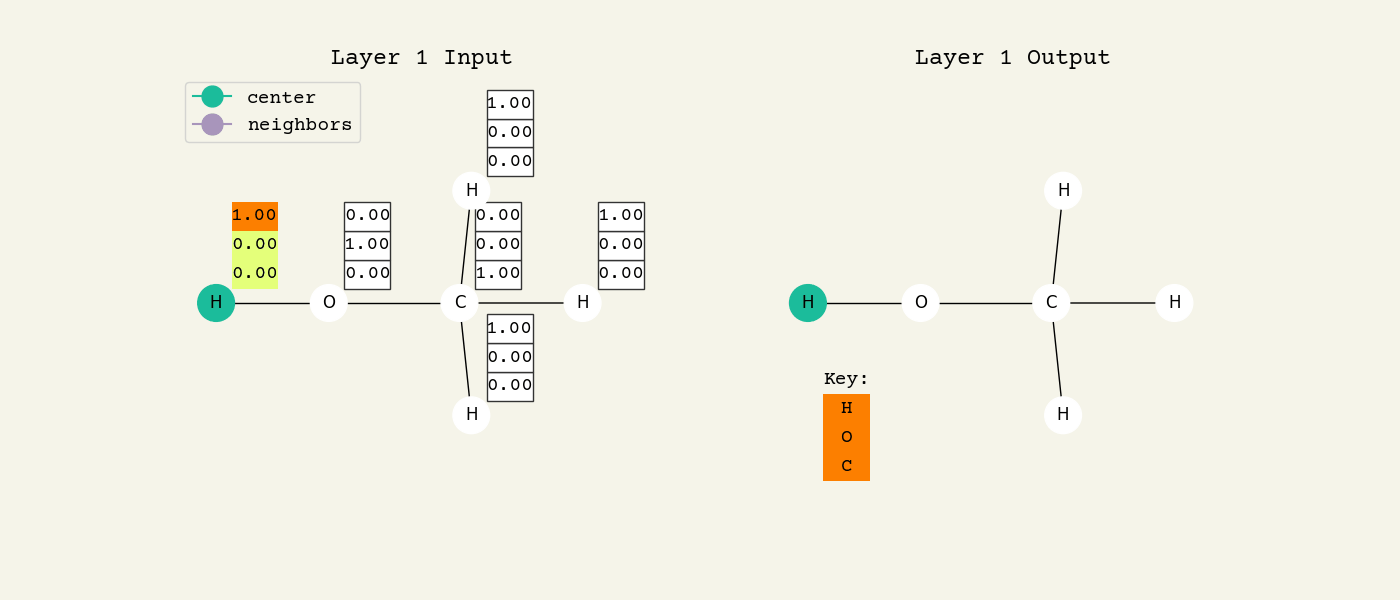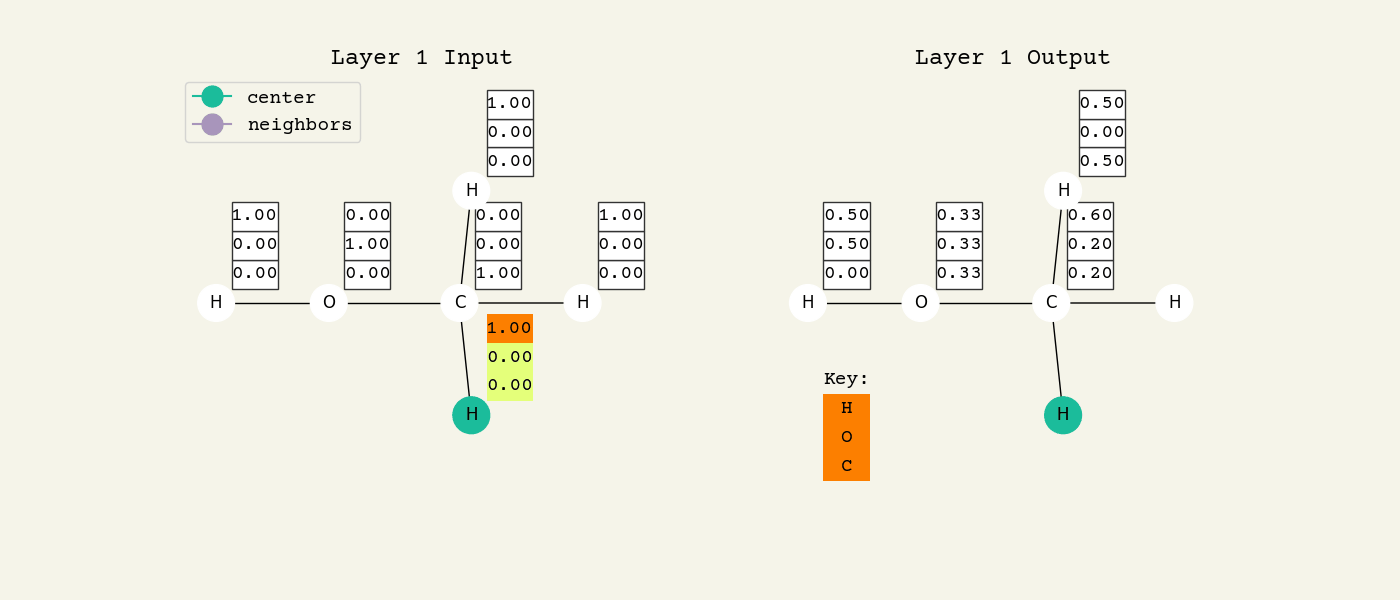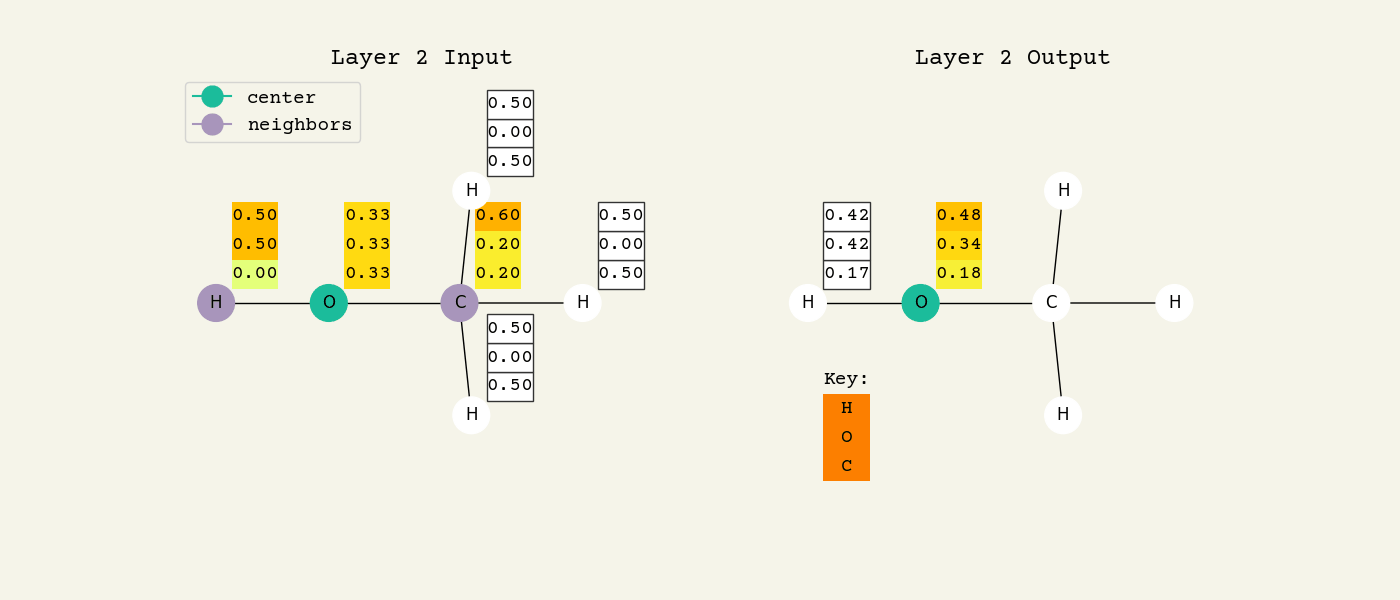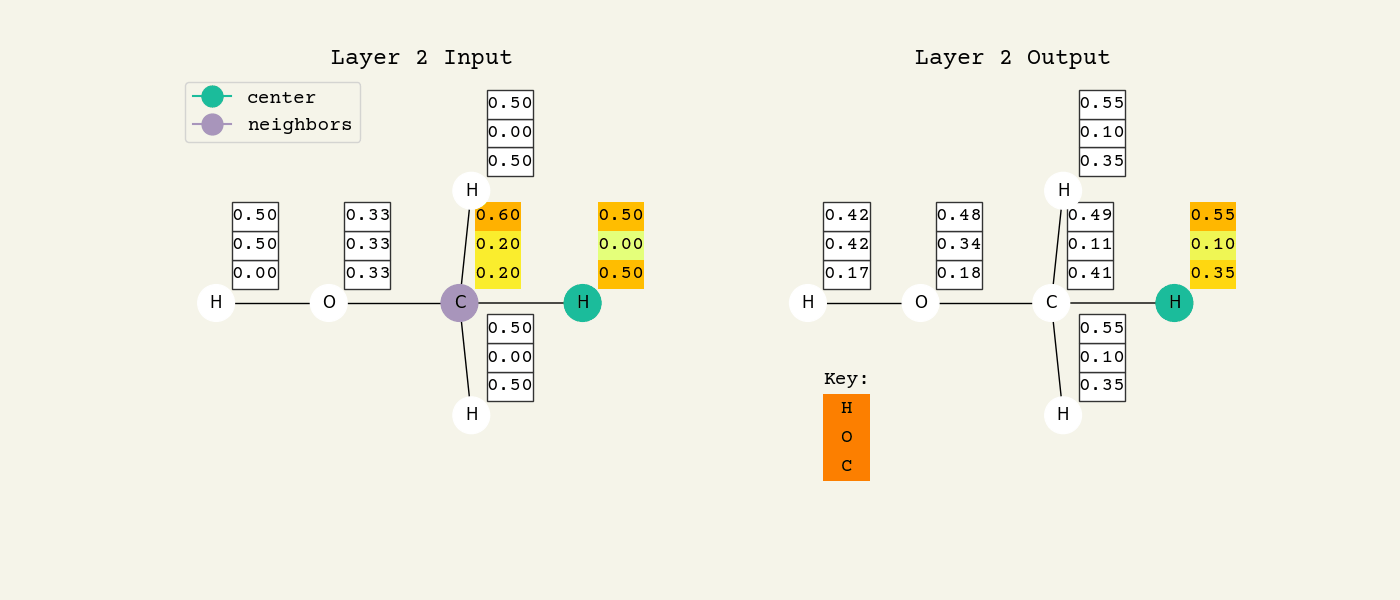
../_images/gcn.gif — Fig. 8.3 グラフ畳み込み層の動作のアニメーション。左が入力、右が出力ノードの特徴です。2つの層が表示されていることに注意してください（タイトルが変わることに注意して見てください）。アニメーションが進むにつれて、近傍ノードの平均化によって、原子についての情報がどのように分子内を伝播していくかがわかることでしょう。つまり、酸素は単なる酸素から、CとHに結合した酸素、HとCH3に結合した酸素へと変化していくのです。図中の色は数値に対応しています。¶

8.4.1. GCNの実装¶

それでは、GCNのテンソル実装を作りましょう。ここでは一旦、活性化関数および学習可能な重みについては省略します。まず最初に、ランク2の隣接行列を計算する必要があります。上の smiles2graph コードは、特徴ベクトルを用いて隣接行列を計算します。この計算は簡単です。同時に恒等行列を加えることにします（訳注：この恒等行列を加算する操作は、上で述べたように自分自身を隣接ノードとして取り扱うための工夫です）。

nodes, adj = smiles2graph("CO")
adj_mat = np.sum(adj, axis=-1) + np.eye(adj.shape[0])
adj_mat

array([[1., 1., 1., 1., 1., 0.],
       [1., 1., 0., 0., 0., 1.],
       [1., 0., 1., 0., 0., 0.],
       [1., 0., 0., 1., 0., 0.],
       [1., 0., 0., 0., 1., 0.],
       [0., 1., 0., 0., 0., 1.]])

各ノードの次数を計算するために、また別な縮約操作を行います：

degree = np.sum(adj_mat, axis=-1)
degree

array([5., 3., 2., 2., 2., 2.])

これでノードの更新操作の準備ができました。アインシュタインの縮約記法を使って更新操作を表現すると次のようになります

print(nodes[0])
# note to divide by degree, make the input 1 / degree
new_nodes = np.einsum("i,ij,jk->ik", 1 / degree, adj_mat, nodes)
print(new_nodes[0])

[1. 0. 0.]
[0.2 0.2 0.6]

これをKerasのLayerとして実装するには、上記のコードを新しいLayerのサブクラスとして記述する必要があります。今回のコードは比較的簡単ですが、Kerasの関数名とLayerクラスについて、このチュートリアルを読んで学ぶことを推奨します。主な変更点は、学習可能なパラメータ self.w を作って tf.einsum の中で用いること、活性化関数 self.activation を用いること、そして新しいノード特徴と隣接行列を出力することの3点です。隣接行列を出力する理由は、隣接行列を毎回渡すことなく、複数のGCNレイヤーをスタックできるようにするためです。

class GCNLayer(tf.keras.layers.Layer):
    """Implementation of GCN as layer"""

    def __init__(self, activation=None, **kwargs):
        # constructor, which just calls super constructor
        # and turns requested activation into a callable function
        super(GCNLayer, self).__init__(**kwargs)
        self.activation = tf.keras.activations.get(activation)

    def build(self, input_shape):
        # create trainable weights
        node_shape, adj_shape = input_shape
        self.w = self.add_weight(shape=(node_shape[2], node_shape[2]), name="w")

    def call(self, inputs):
        # split input into nodes, adj
        nodes, adj = inputs
        # compute degree
        degree = tf.reduce_sum(adj, axis=-1)
        # GCN equation
        new_nodes = tf.einsum("bi,bij,bjk,kl->bil", 1 / degree, adj, nodes, self.w)
        out = self.activation(new_nodes)
        return out, adj

上記のコードの大半はKeras/TFに固有のもので、変数を適切な場所に配置しています。ここで重要なのは2行だけです。1つめは、隣接行列の列について合計することでグラフの次数を計算する操作です：

degree = tf.reduce_sum(adj, axis=-1)

2つめの重要な行は、GCN方程式 (8.3) を計算する部分です（ここでは活性化は省略しています）：

new_nodes = tf.einsum("bi,bij,bjk,kl->bil", 1 / degree, adj, nodes, self.w)

これで、いま実装したGCNレイヤーを試すことができるようになりました：

gcnlayer = GCNLayer("relu")
# we insert a batch axis here
gcnlayer((nodes[np.newaxis, ...], adj_mat[np.newaxis, ...]))

(<tf.Tensor: shape=(1, 6, 3), dtype=float32, numpy=
 array([[[0.        , 0.46567526, 0.07535715],
         [0.        , 0.12714943, 0.05325063],
         [0.01475453, 0.295794  , 0.39316285],
         [0.01475453, 0.295794  , 0.39316285],
         [0.01475453, 0.295794  , 0.39316285],
         [0.        , 0.38166213, 0.        ]]], dtype=float32)>,
 <tf.Tensor: shape=(1, 6, 6), dtype=float32, numpy=
 array([[[1., 1., 1., 1., 1., 0.],
         [1., 1., 0., 0., 0., 1.],
         [1., 0., 1., 0., 0., 0.],
         [1., 0., 0., 1., 0., 0.],
         [1., 0., 0., 0., 1., 0.],
         [0., 1., 0., 0., 0., 1.]]], dtype=float32)>)

これにより (1) 新しいノード特徴、(2) 隣接行列が出力されます。このレイヤーを積み重ねて、GCNを複数回適用できることを確認しましょう。

x = (nodes[np.newaxis, ...], adj_mat[np.newaxis, ...])
for i in range(2):
    x = gcnlayer(x)
print(x)

(<tf.Tensor: shape=(1, 6, 3), dtype=float32, numpy=
array([[[0.        , 0.18908624, 0.        ],
        [0.        , 0.        , 0.        ],
        [0.        , 0.145219  , 0.        ],
        [0.        , 0.145219  , 0.        ],
        [0.        , 0.145219  , 0.        ],
        [0.        , 0.        , 0.        ]]], dtype=float32)>, <tf.Tensor: shape=(1, 6, 6), dtype=float32, numpy=
array([[[1., 1., 1., 1., 1., 0.],
        [1., 1., 0., 0., 0., 1.],
        [1., 0., 1., 0., 0., 0.],
        [1., 0., 0., 1., 0., 0.],
        [1., 0., 0., 0., 1., 0.],
        [0., 1., 0., 0., 0., 1.]]], dtype=float32)>)

うまくいきました！しかし、なぜゼロの値があるのでしょうか？これはおそらく、出力に負の値が含まれており、それがReLU活性化を通した際に0になったためでしょう。これはモデルの訓練が不十分なために起きていると考えられ、訓練を重ねることで解決するでしょう

8.5. 例：溶解度予測¶

次に、GCNによる溶解度の予測について説明します。以前に、分子データセットに含まれている特徴量を使って予測モデルを組んだことを思い出してください。いま我々はGCNを使えるようになったので、特徴量に頭を悩ますことなく、分子構造を直接ニューラルネットワークに入力できるようになりました。GCNレイヤーは各ノードについての特徴を出力しますが、溶解度を予測するためには、グラフ全体についての特徴を得る必要があります。このプロセスをさらに洗練する方法については後で説明しますが、ここでは、GCNレイヤー後のすべてのノード特徴の平均を使うことにします。これにより単純かつ順序不変に、ノード特徴をグラフ特徴に変換することができます。この実装は次のとおりです：

class GRLayer(tf.keras.layers.Layer):
    """A GNN layer that computes average over all node features"""

    def __init__(self, name="GRLayer", **kwargs):
        super(GRLayer, self).__init__(name=name, **kwargs)

    def call(self, inputs):
        nodes, adj = inputs
        reduction = tf.reduce_mean(nodes, axis=1)
        return reduction

上のコードで重要な点は、ノードについて平均をとっている(axis=1)次の部分だけです：

reduction = tf.reduce_mean(nodes, axis=1)

この溶解度予測器を完成させるため、いくつかの全結合層を追加して、回帰が行えることを確認しましょう。回帰の場合は最終層の出力がそのまま予測結果となるため、最終層には活性化を適用しないことに注意してください。このモデルは Keras functional API を使って実装されています。

ninput = tf.keras.Input(
    (
        None,
        100,
    )
)
ainput = tf.keras.Input(
    (
        None,
        None,
    )
)
# GCN block
x = GCNLayer("relu")([ninput, ainput])
x = GCNLayer("relu")(x)
x = GCNLayer("relu")(x)
x = GCNLayer("relu")(x)
# reduce to graph features
x = GRLayer()(x)
# standard layers (the readout)
x = tf.keras.layers.Dense(16, "tanh")(x)
x = tf.keras.layers.Dense(1)(x)
model = tf.keras.Model(inputs=(ninput, ainput), outputs=x)

この100はどこから来たのでしょうか？その答えはデータセットに含まれる元素の数にあります。このデータセットは多数の元素を含むため、以前使ったサイズ3のone-hot encodingでは、全ての元素を表現できません。前回はC, H, Oの元素さえ表現できれば十分でしたが、今回はより多数の元素を扱う必要があります。そのため、one-hot encodingのサイズも100に増やすことにしました。これで最大100種類の元素を表現できます。この拡張のために、モデルだけでなくsmiles2graph関数も更新することにしましょう。

def gen_smiles2graph(sml):
    """Argument for the RD2NX function should be a valid SMILES sequence
    returns: the graph
    """
    m = rdkit.Chem.MolFromSmiles(sml)
    m = rdkit.Chem.AddHs(m)
    order_string = {
        rdkit.Chem.rdchem.BondType.SINGLE: 1,
        rdkit.Chem.rdchem.BondType.DOUBLE: 2,
        rdkit.Chem.rdchem.BondType.TRIPLE: 3,
        rdkit.Chem.rdchem.BondType.AROMATIC: 4,
    }
    N = len(list(m.GetAtoms()))
    nodes = np.zeros((N, 100))
    for i in m.GetAtoms():
        nodes[i.GetIdx(), i.GetAtomicNum()] = 1

    adj = np.zeros((N, N))
    for j in m.GetBonds():
        u = min(j.GetBeginAtomIdx(), j.GetEndAtomIdx())
        v = max(j.GetBeginAtomIdx(), j.GetEndAtomIdx())
        order = j.GetBondType()
        if order in order_string:
            order = order_string[order]
        else:
            raise Warning("Ignoring bond order" + order)
        adj[u, v] = 1
        adj[v, u] = 1
    adj += np.eye(N)
    return nodes, adj

nodes, adj = gen_smiles2graph("CO")
model((nodes[np.newaxis], adj_mat[np.newaxis]))

<tf.Tensor: shape=(1, 1), dtype=float32, numpy=array([[0.0107595]], dtype=float32)>

このモデルは1つの数値（スカラー）を出力します。さて、学習可能なデータセットを得るために、いくつか作業が必要です。このデータセットは少し複雑で、特徴はテンソル(\(mathbf{V}, \mathbf{E}\))のタプルなので、データセットは次のようなタプルのタプルになります： \(\left((\mathbf{V}, \mathbf{E}), y\right)\) generatorはPythonの関数で、値を繰り返し返すことができます。ここでは、学習データを1つずつ取り出すためにgeneratorを使います。続いて、これを from_generator tf.data.Dataset コンストラクタに渡します。このコンストラクタでは、入力データのshapeを明示的に指定する必要があります。

def example():
    for i in range(len(soldata)):
        graph = gen_smiles2graph(soldata.SMILES[i])
        sol = soldata.Solubility[i]
        yield graph, sol


data = tf.data.Dataset.from_generator(
    example,
    output_types=((tf.float32, tf.float32), tf.float32),
    output_shapes=(
        (tf.TensorShape([None, 100]), tf.TensorShape([None, None])),
        tf.TensorShape([]),
    ),
)

ここまで来たらもう少しです。これで、いつものようにデータセットをtrain/val/testに分割できます。

test_data = data.take(200)
val_data = data.skip(200).take(200)
train_data = data.skip(400)

そして、いよいよモデルの訓練です

model.compile("adam", loss="mean_squared_error")
result = model.fit(train_data.batch(1), validation_data=val_data.batch(1), epochs=10)

plt.plot(result.history["loss"], label="training")
plt.plot(result.history["val_loss"], label="validation")
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()

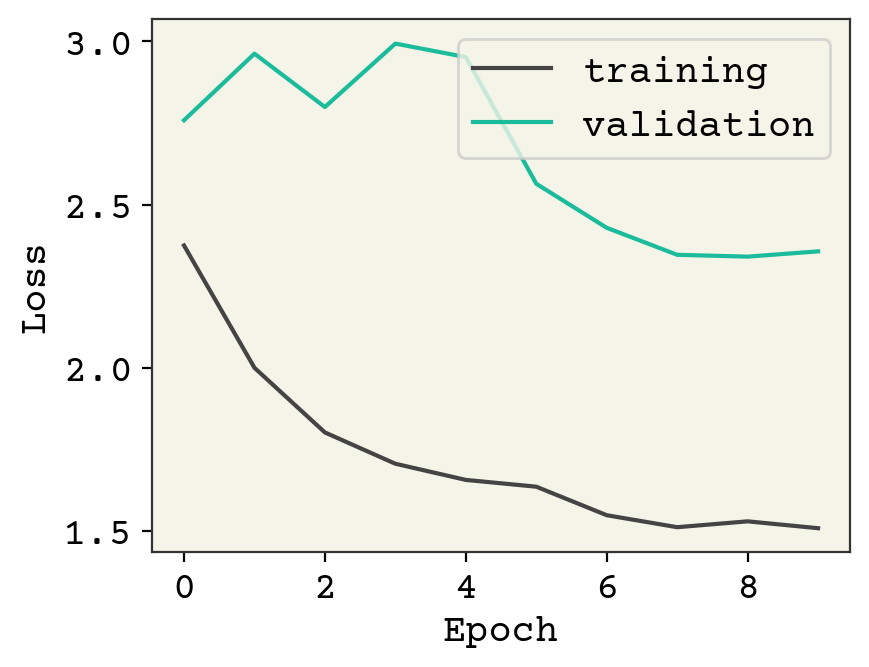
このモデルは明らかにアンダーフィットです。考えられる理由の一つはバッチサイズが1であることです。このモデルでは、原子個数を可変にした副作用としてバッチサイズを1より大きくできない制約があります。もう少し詳しく説明すると、任意のバッチサイズを入力できるようにすると、原子個数とバッチサイズの2つが不定となります。Keras/tensorflowは入力データのshapeに未知の次元が2つ以上ある場合データを処理できないため、バッチサイズを1に固定することで対処しています。ここでは扱いませんが、この問題を回避してバッチサイズを1より大きくするための標準的トリックは、複数の分子を（分子間の結合がない）1つのグラフにまとめてしまうことです。これによりデータの次元はそのままに、分子をバッチ処理することができます。

それではパリティプロットで予測精度を確認してみましょう。

yhat = model.predict(test_data.batch(1), verbose=0)[:, 0]
test_y = [y for x, y in test_data]
plt.figure()
plt.plot(test_y, test_y, "-")
plt.plot(test_y, yhat, ".")
plt.text(
    min(test_y) + 1,
    max(test_y) - 2,
    f"correlation = {np.corrcoef(test_y, yhat)[0,1]:.3f}",
)
plt.text(
    min(test_y) + 1,
    max(test_y) - 3,
    f"loss = {np.sqrt(np.mean((test_y - yhat)**2)):.3f}",
)
plt.title("Testing Data")
plt.show()

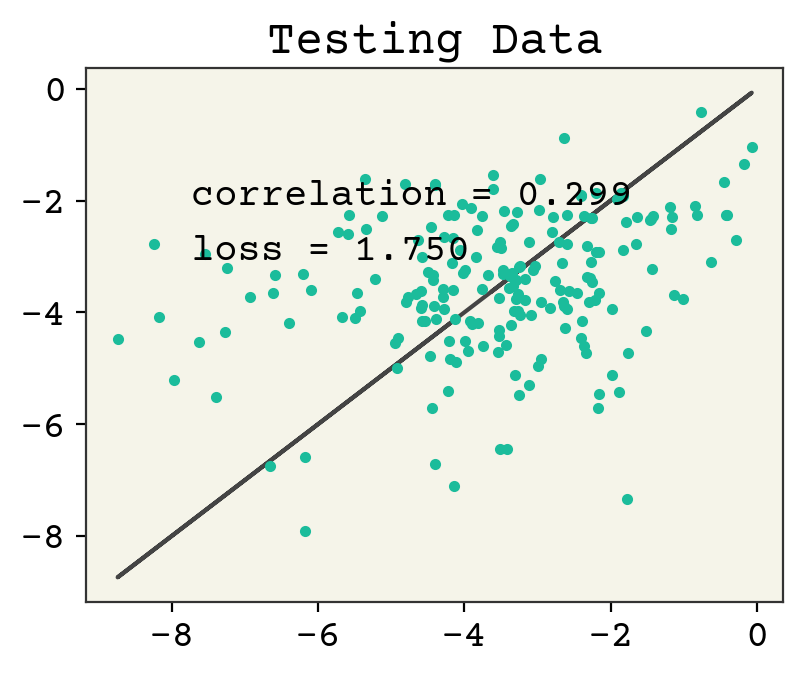
8.6. Message PassingとGCN¶

より広い意味でGCNレイヤーを捉えると、GCNレイヤーは”message-passing”レイヤーの一つと言えます。GCNでは、まず近傍ノードからやってくるメッセージを処理します：

(8.4)¶\[\begin{equation} \vec{e}_{{s_i}j} = \vec{v}_{{s_i}j} \mathbf{W} \end{equation}\]

ここで \(v_{{s_i}j}\) はノード \(i\) の \(j\) 番目の近傍です。 \(s_i\) は \(i\) に対するセンダー（送信者）です。これはGCNがどのようにメッセージを計算するか示したものですが、やっていることは単純で、各近傍ノードの特徴に重み行列をかけているだけです。ノード \(i\) に向かうメッセージ \(\vec{e}_{{s_i}j}\) を得た後、これらのメッセージをノードの順番に対して不変な関数を用いて集約します：

(8.5)¶\[\begin{equation} \vec{e}_{i} = \frac{1}{|\vec{e}_{{s_i}j}|}\sum \vec{e}_{{s_i}j} \end{equation}\]

上で扱ったように、GCNではこの集約は単なる平均ですが、任意の（例えば学習可能な）順序不変の関数を使うこともできます：

(8.6)¶\[\begin{equation} \vec{v}^{'}_{i} = \sigma(\vec{e}_i) \end{equation}\]

\(v^{'}\) は新しいノード特徴を示しています。これは単純に、集約された後で活性化関数を適用したメッセージです。このように書き出すことで、これらの手順にいくらでも小さな変更が加えられることに気づいたのではないでしょうか。Gilmerらによる重要な論文 [GSR+17] では、いくつかの選択肢を検討し、このメッセージパッシングレイヤーの基本的なアイディアが、量子力学に基づいて分子エネルギーを予測するタスクでうまくいくことが述べられています。GCN式に変更を加えた例としては、近傍メッセージの計算においてエッジ特徴を含めたり、単に \(\sigma\) で和をとる代わりに全結合層を使うといった試みが挙げられます。これらから、GCNは、メッセージパッシンググラフニューラルネットワーク（MPNNと略されることもあります）の一種と考えることができます。

8.7. Gated Graph Neural Network¶

メッセージパッシングレイヤーの最も有名な亜種の一つは、 gated graph neural network (GGN) [LTBZ15] です。これは最後の式のノード更新を次で置き換えたものです：

(8.7)¶\[\begin{equation} \vec{v}^{'}_{i} = \textrm{GRU}(\vec{v}_i, \vec{e}_i) \end{equation}\]

\(\textrm{GRU}(\cdot, \cdot)\) はゲート再帰ユニット（gated recurrent unit）[CGCB14] です。 GRU はバイナリ（入力引数を2つ持つ）ニューラルネットワークで、典型的には系列データのモデリングに使用されます。GCNと比較して、GGNの興味深い特徴は、（GRUからの）ノード更新において学習可能なパラメータを持つことで、より柔軟性を備えたモデルとなっていることです。GGNでは、GRUのパラメータは各層で共有されます（GRUを使って系列データをモデリングする方法と同じです）。パラメータ共有によるメリットは、学習すべきパラメータを増やすことなくGGNの層を無限に積み重ねられることです（各層で \(\mathbf{W}\) を揃えることが前提です）。このため、GGNは大きなタンパク質や大きなユニットセルをもつ結晶構造のような、大きなグラフに適しています（訳注：GGNレイヤーを何層もスタックすることで、より遠くのノードからの情報を取り込むことができるためです）。

8.8. Pooling¶

メッセージパッシングの観点、および一般にGNNSでは、近傍からのメッセージを結合する方法が重要なステップとなります。このステップは畳み込みニューラルネットワークで使われるプーリング層に似ているため、プーリングと呼ばれることもあります。畳み込みニューラルネットワークのプーリングと同じように、このために使用できる縮約操作は複数あります。一般的に、GNNのプーリングにはメッセージの合計または平均が使われますが、グラフ同型ネットワーク（Graph Isomorphism Networks） [XHLJ18] のように非常に洗練された操作を用いることもできます。この他にも、例えば注意（attention）の章では自己注意（self-attention）を使う例を扱いますが、これらの操作もプーリングに使えます。プーリングのステップを色々と工夫したくなることもありますが、プーリング操作の選択はモデルの性能にとってそれほど重要ではないことが経験的に分かっています [LDLio19, MSK20]。プーリングの重要な特性は順序不変性で、集約操作はノード（プーリングの場合はエッジ）の順序に依存しない性質を備えることが望まれます。Grattarolaら [GZBA21]が、プーリング手法に関する最近のレビューを出版しています。

Daigavaneらの論文 [DRA21] では、様々なプーリング戦略の比較と概要が視覚的に紹介されています。

8.9. Readout Function¶

GNNの出力はグラフです（そう設計されているので当たり前ですが）。しかし、予測したいラベルもグラフであることは稀で、一般的にはラベルは各ノードまたはグラフ全体に対して付与されています。ノードラベルの例は原子の部分電荷、グラフラベルの例は分子のエネルギーです。GNNから出力されるグラフを、予測ターゲットであるノードラベルやグラフラベルに変換するプロセスを 読み出し（readout） と呼びます。ノードラベルを予測する場合であれば、単純にエッジ特徴を捨てて、GNNから出力されるノード特徴ベクトルを予測結果として扱うことができます。この場合、出力層の前にいくつかの全結合層を挟むことが多いでしょう。

分子のエネルギーや実効電荷のようなグラフレベルのラベルを予測する場合、ノード/エッジ特徴をグラフラベルに変換するプロセスに注意が必要です。所望のshapeのグラフラベルを得るために、単純にノード特徴を全結合層に入力した場合、順序等価性が失われてしまいます（出力はノードラベルではなくグラフラベルなので、厳密には、順序等価性ではなく順序不変性です）。溶解度の例で用いた読み出しは、ノード特徴量に対して縮約操作を行うことでした。その後でグラフ特徴を全結合層に入力して予測結果を得ました。実は、これがグラフ特徴の読み出しを行う唯一の方法であることが示されています [ZKR+17] 。すなわち、グラフ特徴を得るためにノード特徴の縮約操作を行い、このグラフ特徴を全結合層に入力することで予測結果であるグラフラベルを得ます。各ノードの特徴量に対してそれぞれ全結合層を通す操作もできますが、ノード特徴への全結合層の適用はGNN内部で既に行われているので、あまりお勧めしません。このグラフ特徴の読み出しはDeepSetsと呼ばれることもあります。これは、特徴が集合（訳注：順序を持たず、個数が不定）として与えられる場合のために設計された、順序不変なアーキテクチャであるDeepSets [ZKR+17] と同じ形であるためです。

プーリングも読み出しも順序不変の関数が使われていることにお気づきでしょうか。したがって、DeepSetsはプーリングに、attentionは読み出しに使用することもできます。

8.9.1. Intensive vs Extensive¶

回帰タスクでの読み出しにおいて考慮すべき重要な点の1つは、ラベルが intensive か extensive かです。Intensiveラベルは、ノード（＝原子）の数に依存しない値を持つラベルです。例えば、屈折率や溶解度などはIntensiveラベルです。Intensiveラベルの読み出しは、一般にノードの数に依存しないことが要請されます。したがって、この場合の読み出しにおける縮約操作として、平均や最大をとる操作は適用可能ですが、ノード数により値が変わるため合計は適しません。対照的に、Extensiveラベルでは、（一般的には）読み出しの縮約操作には（ノード数を反映できるため）合計が適します。extensiveな分子特性の例には、生成エンタルピーが挙げられます。

8.10. Battaglia General Equations¶

ここまでで学んだように、GNNレイヤーはメッセージパッシングレイヤーとして一般化することができました。Battagliaら [BHB+18] はさらに進んで、ほぼすべてのGNNを記述できる一般的な方程式の集合を考案しました。彼らはGNNレイヤーの方程式を、メッセージパッシングレイヤーの方程式におけるノード更新式のような3つの更新方程式と、3つの集約方程式という合計6つの式に分解しました。これらの式では、グラフ特徴ベクトルという新しい概念が導入されています。このアイディアでは、ネットワークに2つの部分（GNNと読み出し）を持たせる代わりに、グラフレベルの特徴を各GNNレイヤーで更新するアプローチをとります。グラフ特徴ベクトルは、グラフ全体を表す特徴の集合です。例えば溶解度を計算する場合は、読み出し関数を持つ代わりに分子全体の特徴ベクトルを構築し、これを更新して最終的に溶解度を予測する方法が有効だった可能性もあります。このように、分子全体について定義されるあらゆる種類の量（例：溶解度、エネルギー）は、グラフレベルの特徴ベクトルを用いて予測できるでしょう。

これらの式の最初のステップはエッジの特徴ベクトルの更新であり、新たに導入する変数である \(\vec{e}_k\) についての式として記述されます：

(8.8)¶\[ \vec{e}^{'}_k = \phi^e\left( \vec{e}_k, \vec{v}_{rk}, \vec{v}_{sk}, \vec{u}\right) \]

\(\vec{e}_k\) はエッジ \(k\)　の特徴ベクトル、 \(\vec{v}_{rk}\) はエッジ \(k\) について受信されたノード特徴ベクトル、 \(\vec{v}_{sk}\) はエッジ \(k\) についてノード特徴ベクトルを送信したノード、 \(\vec{u}\) はグラフ特徴ベクトル、 \(\phi^e\) はGNNレイヤーの定義に使われる3種類の更新関数のうちの一つです。ただし、ここで言う3種類の更新関数とは一般化した表現であり、必ずしも3種類を定義する必要はありません。ここではそのうちの一つである \(\phi^e\) を用いてGNNレイヤーを定義します。

ここで扱う分子グラフは無向グラフなので、どのノードが \(\vec{v}_{rk}\) を受信し、どのノードが \(\vec{v}_{sk}\) を送信するかをどのように決めれば良いでしょうか？それぞれの \(\vec{e}^{'}_k\) は次のステップでノード \(v_{rk}\) への入力として集約されます。分子グラフでは、全ての結合は原子からの「入力」と「出力」の両方を兼ねるため、全ての結合を2つの有向エッジとして取り扱うことにします（他に良い方法がないのです）：C-H結合はCからHへの辺とHからCへのエッジで構成されることになります。最初の疑問に戻りますが、 \(\vec{v}_{rk} \)と \(\vec{v}_{sk}\) とは何でしょうか？隣接行列のすべての要素（\(k\)）を考え、\(k = \{ij\}\) すなわち要素 \(A_{ij}\) については、受信ノードが \(j\) 、送信ノードが \(i\) であることを表します。逆向きのエッジにおける隣接行列の要素 \(A_{ji}\) を考えると、受信ノードが \(i\) 、送信ノードが \(j\) となります。

\(\vec{e}^{'}_k\) はGCNからのメッセージのようなものですが、より一般的で、受信ノードとグラフ特徴ベクトル \(\vec{u}\) の情報を反映することができます。日常的な意味での「メッセージ」は一度送信されれば誰（あるいは何）に受信されるかによって内容が変わるわけではないので、 \(\vec{e}^{'}_k\) をメッセージの比喩で説明しようとするとおかしなことになります。ともかく、新しいエッジの更新は、最初の集約関数で集約されます：

(8.9)¶\[ \bar{e}^{'}_i = \rho^{e\rightarrow v}\left( E_i^{'}\right) \]

\(\rho^{e\rightarrow v}\) は我々が定義した関数、 \(E_i^{'}\) はノード \(i\) に 向かう 全てのエッジからの \(\vec{e}^{'}_k\) をスタックしたものです。集約されたエッジを使って、ノードの更新を計算できます：

(8.10)¶\[ \vec{v}^{'}_i = \phi^v\left( \bar{e}^{'}_i, \vec{v}_i, \vec{u}\right) \]

以上で新しいノードとエッジが得られたので、GNNレイヤーの通常のステップは完了です。もしグラフ特徴 (\(\vec{u}\)) を更新する場合、以下のステップが追加で定義されることがあります：

(8.11)¶\[ \bar{e}^{'} = \rho^{e\rightarrow u}\left( E^{'}\right) \]

この式は、グラフ全体について全てのメッセージ/集約されたエッジを集約します。これにより、新しいノードをグラフ全体について集約できます：

(8.12)¶\[ \bar{v}^{'} = \rho^{v\rightarrow u}\left( V^{'}\right) \]

そして最後に、次のようにしてグラフ特徴ベクトルを更新できます：

(8.13)¶\[ \vec{u}^{'} = \phi^u\left( \bar{e}^{'},\bar{v}^{'}, \vec{u}\right) \]

8.10.1. Battaglia equationsによるGCNの再定式化¶

Battagliaの式によりGCNがどのように記述されるか見てみましょう。まず (8.8) を使って、隣接する可能性のあるすべての隣接ノードに対してメッセージを計算します。GCNでは、メッセージは送信者にのみ依存し、受信者には依らないことに注意してください。

\[ \vec{e}^{'}_k = \phi^e\left( \vec{e}_k, \vec{v}_{rk}, \vec{v}_{sk}, \vec{u}\right) = \vec{v}_{sk} \mathbf{W} \]

(8.9) においてノード \(i\) にやってくるメッセージを集約するために、これらのメッセージの平均をとります：

\[ \bar{e}^{'}_i = \rho^{e\rightarrow v}\left( E_i^{'}\right) = \frac{1}{|E_i^{'}|}\sum E_i^{'} \]

続いて、ノードの更新を行いますが、これは単にメッセージについて活性化関数を適用するだけです (8.10)

\[ \vec{v}^{'}_i = \phi^v\left( \bar{e}^{'}_i, \vec{v}_i, \vec{u}\right) = \sigma(\bar{e}^{'}_i) \]

上式において \(\sigma(\bar{e}^{'}_i + \vec{v}_i)\) と変更を加えることで、グラフに自己ループを持たせることも可能です。GCNでは他の関数は必要ないので、これら3つの式だけでGCNを定義することができます。

8.11. The SchNet Architecture¶

最も古く、かつよく用いられるGNNの1つに、SchNetネットワーク [SchuttSK+18] があります。発表当時はあまりGNNとしては認識されていませんでしたが、現在ではその一つとして認識され、ベースラインモデルとしてよく使われています。ベースラインモデルとは、新手法との比較に用いられるモデルのことで、広く受け入れられ、かつ様々な実験を通じて良い性能を示すことが確認されているモデルが使われます。

これまでに扱った全ての例では、分子をグラフとしてモデルへ入力していました。一方SchNetでは、分子グラフではなく、原子をxyz座標（点）として表現し入力し、xyz座標をグラフに変換することでGNNNを適用します。SchNetは、結合情報なしで原子の配置のみからエネルギーや力を予測するために開発されました。したがって、SchNetを理解するために、まず原子とその位置のセットがどのようにグラフに変換されるかを確認しましょう。各原子をノード化する手順は簡単で、上記と同様の処理を行った後、原子番号をembeddingレイヤーに渡します。これは、各原子番号に学習可能なベクトルを割り当てること（訳注：学習により、各原子の抽象的特徴を捉えた高次元ベクトルを得ること）を意味します（embeddingについての復習は Standard Layers を参照してください）。

隣接行列の計算も簡単で、全ての原子が全ての原子に接続されるようにするだけです。単に全原子が相互に接続するのだとしたら、GNNを使う意味がよくわからないと思われるかもしれません。このような操作をする理由は、GNNは順序等価であるからです。もし原子をxyz座標として学習しようとすると，原子の並び方によって重みが変わってしまう上に、構造ごとの原子数の違いをうまく取り扱えないことでしょう。

SchNetを理解するためにもう一つ押さえるべき点は、各原子のxyz座標の情報はどう扱われるのか、ということです。SchNetでは、xyz座標からエッジ特徴を構築することにより、モデルに座標の情報を取り込んでいます。原子 \(i\) と \(j\) の間のエッジ \(\vec{e}\) は、シンプルにこれらの原子間距離 \(r\) から計算されます。

(8.14)¶\[ e_k = \exp\left(-\gamma \left(r - \mu_k\right)^2\right) \]

\(\gamma\) はハイパーパラメータ（例： 10Å） \(\mu_k\) は [0, 5, 10, 15 , 20] のようなスカラーの等間隔グリッドです。 (8.14) の操作は、原子番号や共有結合の種類のようなカテゴリ特徴をone-hotベクトルに変換することに似ています。しかし、カテゴリカルな量と異なり、距離は連続値で無限にあるので、one-hotベクトルとして表現することはできません。そこで、一種の「スムージング」によって、距離を擬似的にone-hot表現しているのです。この感覚をつかむために、例を見てみましょう：

gamma = 1
mu = np.linspace(0, 10, 5)


def rbf(r):
    return np.exp(-gamma * (r - mu) ** 2)


print("input", 2)
print("output", np.round(rbf(2), 2))

input 2
output [0.02 0.78 0.   0.   0.  ]

距離　\(r=2\) は、 \(k = 1\)　の位置（訳注：kはこのlistのindexのことです）が強く活性化したベクトルを与えることがわかります。これは \(\mu_1 = 2\) であることに対応します。

ここまででノードとエッジおよび、GNNの更新方程式を定義しました。さらにもう少しだけ記号を定義しておく必要があります。ここでは、MLP（Multilayer perceptron）を表すために \(h(\vec{x})\) を使用します。MLPは、基本的に1層あるいは2層の全結合レイヤーからなるニューラルネットワークです。これらのMLPにおける全結合レイヤーの正確な数や、いつ・どこで活性化を行うかといった詳細は、重要な点を理解する上で不要なため説明は省略します（これらの詳細は以下の実装例を参照してください）。ではここで、全結合レイヤーの定義を思い出しましょう：

\[ h(\vec{x}) = \sigma\left(Wx + b\right) \]

また、SchNetでは “shifted softplus” と呼ばれる新たな活性化関数 \(\sigma\) を用います： \(\sigma = \ln\left(0.5e^{x} + 0.5\right)\) 。 Fig. 8.4 において、 \(\sigma(x)\) と通常のReLU活性化を比較した分析が報告されています。shifted softplusを使う理由は、入力に対して滑らかであるためです。このため、粒子同士の距離（pairwise distance）に対して滑らかな微分が必要とされる分子動力学シミュレーションのようなアプリケーションにおいて、フォース（訳注：粒子同士に働く力）を計算するためにSchNetを使うことができます。

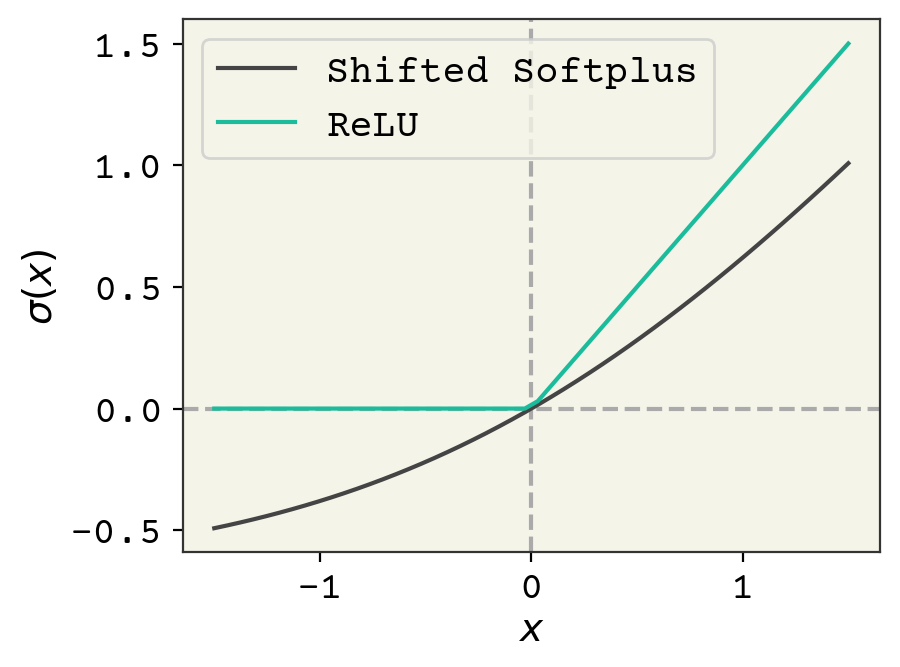
../_images/gnn_49_0.png — Fig. 8.4 一般的なReLU活性化関数と、SchNetで使用されているshifted softplusの比較¶

さて、前置きが続きましたが、ようやくGNN方程式に話を移します。エッジの更新方程式 (8.8) は2つの部分から成ります。まず、やってくるエッジ（＝結合）特徴と、ノード（＝原子）の特徴をMLPに通します。続いて、それらの結果を次のMLPに通します：

\[ \vec{e}^{'}_k = \phi^e\left( \vec{e}_k, \vec{v}_{rk}, \vec{v}_{sk}, \vec{u}\right) =h_1\left(\vec{v}_{sk}\right) \cdot h_2\left(\vec{e}_k\right) \]

次にエッジの集約関数 (8.9) を考えましょう。SchNetでは、エッジ集約は近傍の原子特徴量に対する和です。

\[ \bar{e}^{'}_i = \sum E_i^{'} \]

最後に、SchNetのノード更新関数は以下のようになります：

\[ \vec{v}^{'}_i = \phi^v\left( \bar{e}^{'}_i, \vec{v}_i, \vec{u}\right) = \vec{v}_i + h_3\left(\bar{e}^{'}_i\right) \]

通常、GNNの更新は3〜6回適用されます。上記のSchNetの説明において、エッジの更新式を定義しましたが、GCN同様に実際にはエッジ特徴を上書きせず、各層で同じエッジ特徴が保たれます。元々のSchNetはエネルギーや力を予測するためのものなので、読み出しはsum-poolingや上記のような戦略で行うことが可能です。

これらの式の詳細は変更されることもありますが、オリジナルのSchNetの論文では、 \(h_1\) は活性化なしのdenseな1層、\(h_2\) は活性化ありの2層、\(h_3\) は1層に活性化あり・2層目は活性化無しのdenseな2層の構成が用いられました。

SchNetとは?

SchNetベースのGNNの主な特徴は、（1）エッジの更新（メッセージの組み立て）にエッジとノードの特徴を用いることです：

\[ \vec{e}^{'}_k = h_1(\vec{v}_{sk}) \cdot h_2(\vec{e}_k) \]

ここで \(h_i()\) は何らかの学習可能な関数です。特徴（2）は、ノード更新に残差を利用することです：

\[ \vec{v}^{'}_i = \vec{v}_i + h_3\left(\bar{e}^{'}_i\right) \]

その他、エッジ特徴の作り方、\(h_i\) の層数、活性化関数の選択、読み出しの方法、ポイントクラウドをグラフに変換する方法など、詳細は全て [SchuttSK+18] で提案されたSchNetモデルの定義に準拠します。

8.12. SchNet Example: Predicting Space Groups¶

Our next example will be a SchNet model that predict space groups of points. Identifying the space group of atoms is an important part of crystal structure identification, and when doing simulations of crystallization. Our SchNet model will take as input points and output the predicted space group. This is a classification problem; specifically it is multi-class becase a set of points should only be in one space group. To simplify our plots and analysis, we will work in 2D where there are 17 possible space groups.

Our data for this is a set of points from various point groups. The features are xyz coordinates and the label is the space group. We will not have multiple atom types for this problem. The hidden cell below loads the data and reshapes it for the example.

import gzip
import pickle
import urllib

urllib.request.urlretrieve(
    "https://github.com/whitead/dmol-book/raw/master/data/sym_trajs.pb.gz",
    "sym_trajs.pb.gz",
)
with gzip.open("sym_trajs.pb.gz", "rb") as f:
    trajs = pickle.load(f)

label_str = list(set([k.split("-")[0] for k in trajs]))

# now build dataset
def generator():
    for k, v in trajs.items():
        ls = k.split("-")[0]
        label = label_str.index(ls)
        traj = v
        for i in range(traj.shape[0]):
            yield traj[i], label


data = tf.data.Dataset.from_generator(
    generator,
    output_signature=(
        tf.TensorSpec(shape=(None, 2), dtype=tf.float32),
        tf.TensorSpec(shape=(), dtype=tf.int32),
    ),
).shuffle(1000)

# The shuffling above is really important because this dataset is in order of labels!

val_data = data.take(100)
test_data = data.skip(100).take(100)
train_data = data.skip(200)

Let’s take a look at a few examples from the dataset

The Data

This data was generated from [CW22] and all points are constrained to match the space group exactly during a molecular dynamics simulation. The trajectories were NPT with a positive pressure and followed the procedure in that paper for Figure 2. The force field is Lennard-Jones with \(\sigma=1\) and \(\epsilon=1\)

fig, axs = plt.subplots(4, 5, figsize=(12, 8))
axs = axs.flatten()

# get a few example and plot them
for i, (x, y) in enumerate(data):
    if i == 20:
        break
    axs[i].plot(x[:, 0], x[:, 1], ".")
    axs[i].set_title(label_str[y.numpy()])
    axs[i].axis("off")

You can see that there is a variable number of points and a few examples for each space group. The goal is to infer those titles on the plot from the points alone.

8.12.1. Building the graphs¶

We now need to build the graphs for the points. The nodes are all identical - so they can just be 1s (we’ll reserve 0 in case we want to mask or pad at some point in the future). As described in the SchNet section above, the edges should be distance to every other atom. In most implementations of SchNet, we practically add a cut-off on either distance or maximum degree (edges per node). We’ll do maximum degree for this work of 16.

I have a function below that is a bit sophisticated. It takes a matrix of point positions in arbitrary dimension and returns the distances and indices to the nearest k neighbors - exactly what we need. It uses some tricks from Tensors and Shapes. However, it is not so important for you to understand this function. Just know it takes in points and gives us the edge features and edge nodes.

# this decorator speeds up the function by "compiling" it (tracing it)
# to run efficienty
@tf.function(
    reduce_retracing=True,
)
def get_edges(positions, NN, sorted=True):
    M = tf.shape(input=positions)[0]
    # adjust NN
    NN = tf.minimum(NN, M)
    qexpand = tf.expand_dims(positions, 1)  # one column
    qTexpand = tf.expand_dims(positions, 0)  # one row
    # repeat it to make matrix of all positions
    qtile = tf.tile(qexpand, [1, M, 1])
    qTtile = tf.tile(qTexpand, [M, 1, 1])
    # subtract them to get distance matrix
    dist_mat = qTtile - qtile
    # mask distance matrix to remove zros (self-interactions)
    dist = tf.norm(tensor=dist_mat, axis=2)
    mask = dist >= 5e-4
    mask_cast = tf.cast(mask, dtype=dist.dtype)
    # make masked things be really far
    dist_mat_r = dist * mask_cast + (1 - mask_cast) * 1000
    topk = tf.math.top_k(-dist_mat_r, k=NN, sorted=sorted)
    return -topk.values, topk.indices

Let’s see how this function works by showing the connections between points in one of our examples. I’ve hidden the code below. It shows some point’s neighbors and connects them so you can get a sense of how a set of points is converted into a graph. The complete graph will have all points’ neighborhoods.

from matplotlib import collections

fig, axs = plt.subplots(2, 3, figsize=(12, 8))
axs = axs.flatten()
for i, (x, y) in enumerate(data):
    if i == 6:
        break
    e_f, e_i = get_edges(x, 8)

    # make things easier for plotting
    e_i = e_i.numpy()
    x = x.numpy()
    y = y.numpy()

    # make lines from origin to its neigbhors
    lines = []
    colors = []
    for j in range(0, x.shape[0], 23):
        # lines are [(xstart, ystart), (xend, yend)]
        lines.extend([[(x[j, 0], x[j, 1]), (x[k, 0], x[k, 1])] for k in e_i[j]])
        colors.extend([f"C{j}"] * len(e_i[j]))
    lc = collections.LineCollection(lines, linewidths=2, colors=colors)
    axs[i].add_collection(lc)
    axs[i].plot(x[:, 0], x[:, 1], ".")
    axs[i].axis("off")
    axs[i].set_title(label_str[y])
plt.show()

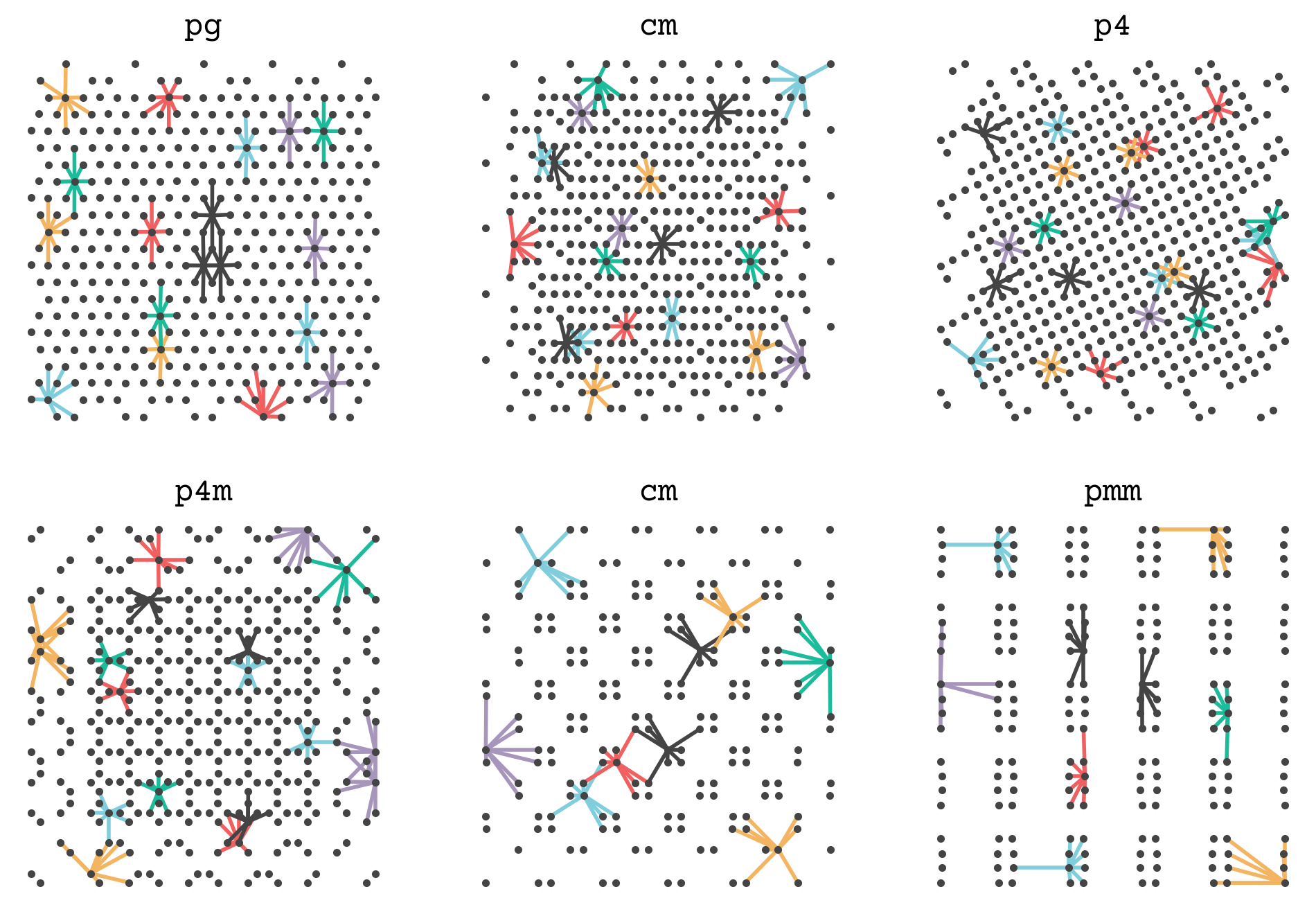
We will now add this function and the edge featurization of SchNet (8.14) to get the graphs for the GNN steps.

MAX_DEGREE = 16
EDGE_FEATURES = 8
MAX_R = 20

gamma = 1
mu = np.linspace(0, MAX_R, EDGE_FEATURES)


def rbf(r):
    return tf.exp(-gamma * (r[..., tf.newaxis] - mu) ** 2)


def make_graph(x, y):
    edge_r, edge_i = get_edges(x, MAX_DEGREE)
    edge_features = rbf(edge_r)
    return (tf.ones(tf.shape(x)[0], dtype=tf.int32), edge_features, edge_i), y[None]


graph_train_data = train_data.map(make_graph)
graph_val_data = val_data.map(make_graph)
graph_test_data = test_data.map(make_graph)

Let’s examine one graph to see what it looks like. We’ll slice out only the first nodes.

for (n, e, nn), y in graph_train_data:
    print("first node:", n[1].numpy())
    print("first node, first edge features:", e[1, 1].numpy())
    print("first node, all neighbors", nn[1].numpy())
    print("label", y.numpy())
    break

first node: 1
first node, first edge features: [2.8479335e-01 4.9036104e-02 6.8545725e-10 7.7790052e-25 0.0000000e+00
 0.0000000e+00 0.0000000e+00 0.0000000e+00]
first node, all neighbors [  7  11  10 206   4  12 197   9  13  15   3 192 200   2 130 195]
label [13]

8.12.2. Implementing the MLPs¶

Now we can implement the SchNet model! Let’s start with the \(h_1,h_2,h_3\) MLPs that are used in the GNN update equations. In the SchNet paper these each had different numbers of layers and different decisions about which layers had activation. Let’s create them now.

def ssp(x):
    # shifted softplus activation
    return tf.math.log(0.5 * tf.math.exp(x) + 0.5)


def make_h1(units):
    return tf.keras.Sequential([tf.keras.layers.Dense(units)])


def make_h2(units):
    return tf.keras.Sequential(
        [
            tf.keras.layers.Dense(units, activation=ssp),
            tf.keras.layers.Dense(units, activation=ssp),
        ]
    )


def make_h3(units):
    return tf.keras.Sequential(
        [tf.keras.layers.Dense(units, activation=ssp), tf.keras.layers.Dense(units)]
    )

One detail that can be missed is that the weights in each MLP should change in each layer of SchNet. Thus, we’ve written the functions above to always return a new MLP. This means that a new set of trainable weights is generated on each call, meaning there is no way we could erroneously have the same weights in multiple layers.

8.12.3. Implementing the GNN¶

Now we have all the pieces to make the GNN. This code will be very similar to the GCN example above, except we now have edge features. One more detail is that our readout will be an MLP as well, following the SchNet paper. The only change we’ll make is that we want our output property to be (1) multi-class classification and (2) intensive (independent of number of atoms). So we’ll end with an average (intensive) and end with an output vector of logits the size of our labels.

class SchNetModel(tf.keras.Model):
    """Implementation of SchNet Model"""

    def __init__(self, gnn_blocks, channels, label_dim, **kwargs):
        super(SchNetModel, self).__init__(**kwargs)
        self.gnn_blocks = gnn_blocks

        # build our layers
        self.embedding = tf.keras.layers.Embedding(2, channels)
        self.h1s = [make_h1(channels) for _ in range(self.gnn_blocks)]
        self.h2s = [make_h2(channels) for _ in range(self.gnn_blocks)]
        self.h3s = [make_h3(channels) for _ in range(self.gnn_blocks)]
        self.readout_l1 = tf.keras.layers.Dense(channels // 2, activation=ssp)
        self.readout_l2 = tf.keras.layers.Dense(label_dim)

    def call(self, inputs):
        nodes, edge_features, edge_i = inputs
        # turn node types as index to features
        nodes = self.embedding(nodes)
        for i in range(self.gnn_blocks):
            # get the node features per edge
            v_sk = tf.gather(nodes, edge_i)
            e_k = self.h1s[i](v_sk) * self.h2s[i](edge_features)
            e_i = tf.reduce_sum(e_k, axis=1)
            nodes += self.h3s[i](e_i)
        # readout now
        nodes = self.readout_l1(nodes)
        nodes = self.readout_l2(nodes)
        return tf.reduce_mean(nodes, axis=0)

Remember that the key attributes of a SchNet GNN are the way that we use edge and node features. We can see the mixing of these two in the key line for computing the edge update (computing message values):

e_k = self.h1s[i](v_sk) * self.h2s[i](edge_features)

followed by aggregation of the edges updates (pooling messages):

e_i = tf.reduce_sum(e_k, axis=1)

and the node update

nodes += self.h3s[i](e_i)

Also of note is how we go from node features to multi-classs. We use dense layers that get the shape per-node into the number of classes

self.readout_l1 = tf.keras.layers.Dense(channels // 2, activation=ssp)
self.readout_l2 = tf.keras.layers.Dense(label_dim)

and then we take the average over all nodes

return tf.reduce_mean(nodes, axis=0)

Let’s give now use the model on some data.

small_schnet = SchNetModel(3, 32, len(label_str))

for x, y in graph_train_data:
    yhat = small_schnet(x)
    break
print(yhat.numpy())

[ 0.01385795  0.00906286  0.00222304 -0.00563365  0.00490831  0.00621619
  0.02778318  0.0169939  -0.00951115 -0.00167371 -0.0171227  -0.00270679
 -0.00358437  0.00626842 -0.00611755  0.01474886  0.01494901]

The output is the correct shape and remember it is logits. To get a class prediction that sums to probability 1, we need to use a softmax:

print("predicted class", tf.nn.softmax(yhat).numpy())

predicted class [0.05939336 0.05910925 0.05870633 0.0582469  0.05886419 0.05894123
 0.06022622 0.05957991 0.05802149 0.05847801 0.05758153 0.05841763
 0.05836639 0.0589443  0.05821873 0.0594463  0.0594582 ]

8.12.4. Training¶

Great! It is untrained though. Now we can set-up training. Our loss will be cross-entropy from logits, but we need to be careful on the form. Our labels are integers - which is called “sparse” labels because they are not full one-hots. Mult-class classification is also known as categorical classification. Thus, the loss we want is sparse categorical cross entropy from logits.

small_schnet.compile(
    optimizer=tf.keras.optimizers.Adam(1e-4),
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    metrics="sparse_categorical_accuracy",
)
result = small_schnet.fit(graph_train_data, validation_data=graph_val_data, epochs=20)

plt.plot(result.history["sparse_categorical_accuracy"], label="training accuracy")
plt.plot(result.history["val_sparse_categorical_accuracy"], label="validation accuracy")
plt.axhline(y=1 / 17, linestyle="--", label="random")
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Accuracy")
plt.show()

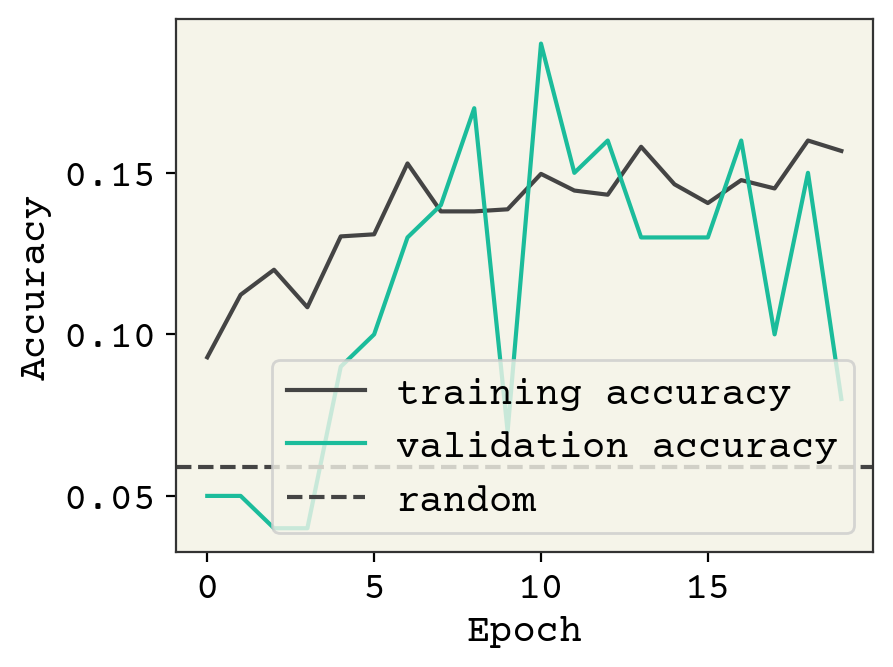
The accuracy is not great, but it looks like we could keep training. We have a very small SchNet here. Standard SchNet described in [SchuttSK+18] uses 6 layers and 64 channels and 300 edge features. We have 3 layers and 32 channels. Nevertheless, we’re able to get some learning. Let’s visually see what’s going on with the trained model on some test data

fig, axs = plt.subplots(4, 5, figsize=(12, 8))
axs = axs.flatten()

for i, ((x, y), (gx, _)) in enumerate(zip(test_data, graph_test_data)):
    if i == 20:
        break
    axs[i].plot(x[:, 0], x[:, 1], ".")
    yhat = small_schnet(gx)
    yhat_i = tf.math.argmax(tf.nn.softmax(yhat)).numpy()
    axs[i].set_title(f"True: {label_str[y.numpy()]}\nPredicted: {label_str[yhat_i]}")
    axs[i].axis("off")
plt.tight_layout()
plt.show()

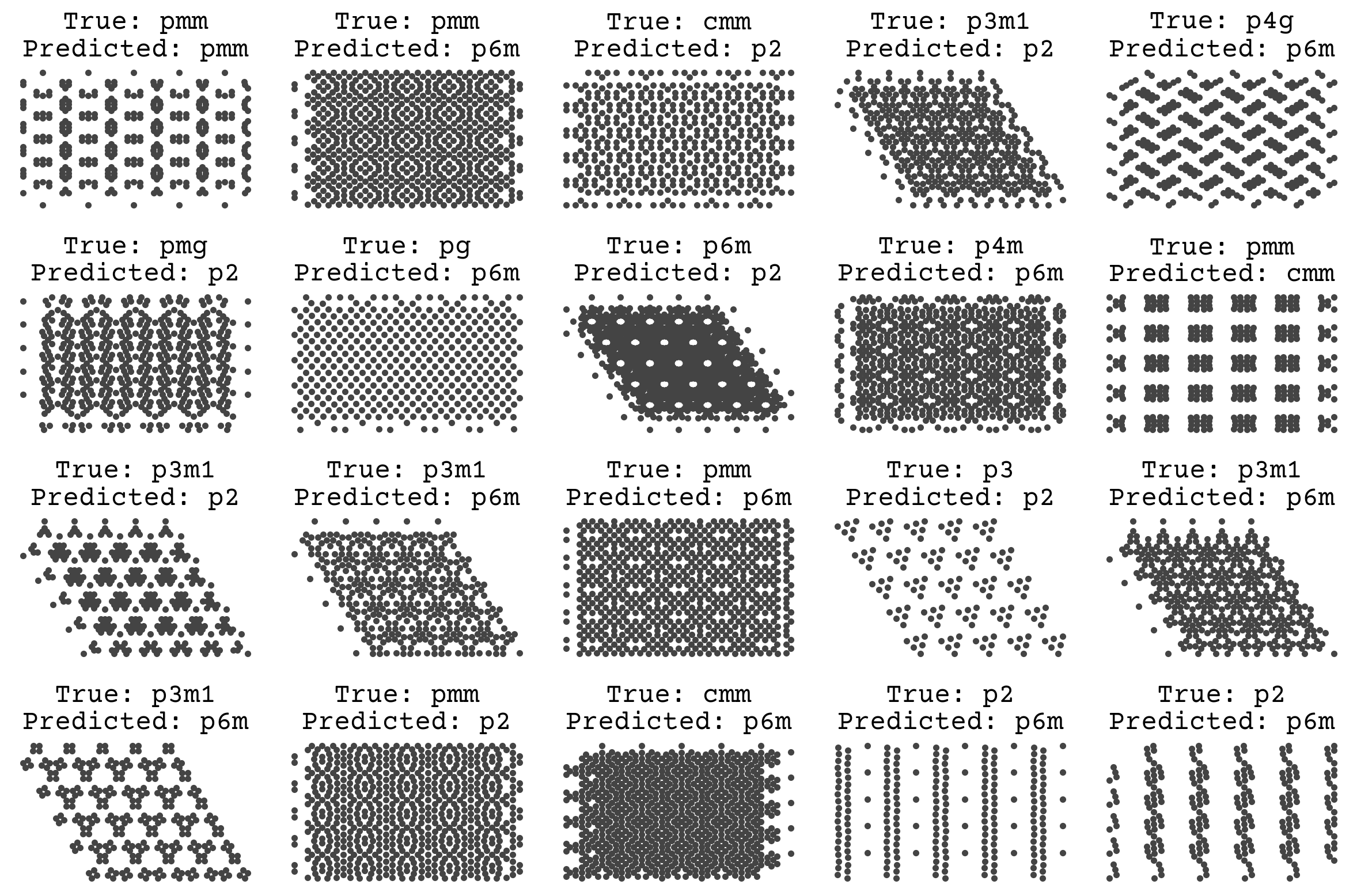
We’ll revisit this example later! One unique fact about this dataset is that it is synthetic, meaning there is no label noise. As discussed in Regression & Model Assessment, that removes the possibility of overfitting and leads us to favor high variance models. The goal of teaching a model to predict space groups is to apply it on real simulations or microscopy data, which will certainly have noise. We could have mimicked this by adding noise to the labels in the data and/or by randomly removing atoms to simulate defects. This would better help our model work in a real setting.

8.13. Current Research Directions¶

8.13.1. Common Architecture Motifs and Comparisons¶

We’ve now seen message passing layer GNNs, GCNs, GGNs, and the generalized Battaglia equations. You’ll find common motifs in the architectures, like gating, アテンションレイヤー, and pooling strategies. For example, Gated GNNS (GGNs) can be combined with attention pooling to create Gated Attention GNNs (GAANs)[ZSX+18]. GraphSAGE is a similar to a GCN but it samples when pooling, making the neighbor-updates of fixed dimension[HYL17]. So you’ll see the suffix “sage” when you sample over neighbors while pooling. These can all be represented in the Battaglia equations, but you should be aware of these names.

The enormous variety of architectures has led to work on identifying the “best” or most general GNN architecture [DJL+20, EPBM19, SMBGunnemann18]. Unfortunately, the question of which GNN architecture is best is as difficult as “what benchmark problems are best?” Thus there are no agreed-upon conclusions on the best architecture. However, those papers are great resources on training, hyperparameters, and reasonable starting guesses and I highly recommend reading them before designing your own GNN. There has been some theoretical work to show that simple architectures, like GCNs, cannot distinguish between certain simple graphs [XHLJ18]. How much this practically matters depends on your data. Ultimately, there is so much variety in hyperparameters, data equivariances, and training decisions that you should think carefully about how much the GNN architecture matters before exploring it with too much depth.

8.13.2. Nodes, Edges, and Features¶

You’ll find that most GNNs use the node-update equation in the Battaglia equations but do not update edges. For example, the GCN will update nodes at each layer but the edges are constant. Some recent work has shown that updating edges can be important for learning when the edges have geometric information, like if the input graph is a molecule and the edges are distance between the atoms [KGrossGunnemann20]. As we’ll see in the chapter on equivariances (Input Data & Equivariances), one of the key properties of neural networks with point clouds (i.e., Cartesian xyz coordinates) is to have rotation equivariance. [KGrossGunnemann20] showed that you can achieve this if you do edge updates and encode the edge vectors using a rotation equivariant basis set with spherical harmonics and Bessel functions. These kind of edge updating GNNs can be used to predict protein structure [JES+20].

Another common variation on node features is to pack more into node features than just element identity. In many examples, you will see people inserting valence, elemental mass, electronegativity, a bit indicating if the atom is in a ring, a bit indicating if the atom is aromatic, etc. Typically these are unnecessary, since a model should be able to learn any of these features which are computed from the graph and node elements. However, we and others have empirically found that some can help, specifically indicating if an atom is in a ring [LWC+20]. Choosing extra features to include though should be at the bottom of your list of things to explore when designing and using GNNs.

8.13.3. Beyond Message Passing¶

One of the common themes of GNN research is moving “beyond message passing,” where message passing is the message construction, aggregation, and node update with messages. Some view this as impossible – claiming that all GNNs can be recast as message passing [Velivckovic22]. Another direction is on disconnecting the underlying graph being input to the GNN and the graph used to compute updates. We sort of saw this above with SchNet, where we restricted the maximum degree for the message passing. More useful are ideas like “lifting” the graphs into more structured objects like simplicial complexes [BFO+21]. Finally, you can also choose where to send the messages beyond just neighbors [TZK21]. For example, all nodes on a path could communicate messages or all nodes in a clique.

8.13.4. Do we need graphs?¶

It is possible to convert a graph into a string if you’re working with an adjacency matrix without continuous values. Molecules specifically can be converted into a string. This means you can use layers for sequences/strings (e.g., recurrent neural networks or 1D convolutions) and avoid the complexities of a graph neural network. SMILES is one way to convert molecular graphs into strings. With SMILES, you cannot predict a per-atom quantity and thus a graph neural network is required for atom/bond labels. However, the choice is less clear for per-molecule properties like toxicity or solubility. There is no consensus about if a graph or string/SMILES representation is better. SMILES can exceed certain graph neural networks in accuracy on some tasks. SMILES is typically better on generative tasks. Graphs obviously beat SMILES in label representations, because they have granularity of bonds/edges. We’ll see how to model SMILES in Deep Learning on Sequences, but it is an open question of which is better.

8.13.5. Stereochemistry/Chiral Molecules¶

Stereochemistry is fundamentally a 3D property of molecules and thus not present in the covalent bonding. It is measured experimentally by seeing if molecules rotate polarized light and a molecule is called chiral or “optically active” if it is experimentally known to have this property. Stereochemistry is the categorization of how molecules can preferentially rotate polarized light through asymmetries with respect to their mirror images. In organic chemistry, the majority of stereochemistry is of enantiomers. Enantiomers are “handedness” around specific atoms called chiral centers which have 4 or more different bonded atoms. These may be treated in a graph by indicating which nodes are chiral centers (nodes) and what their state or mixture of states (racemic) are. This can be treated as an extra processing step. Amino acids and thus all proteins are entaniomers with only one form present. This chirality of proteins means many drug molecules can be more or less potent depending on their stereochemistry.

../_images/helicene.mp4

Fig. 8.5 This is a molecule with axial stereochemistry. Its small helix could be either left or right-handed.¶

Adding node labels is not enough generally. Molecules can interconvert between stereoisomers at chiral centers through a process called tautomerization. There are also types of stereochemistry that are not at a specific atom, like rotamers that are around a bond. Then there is stereochemistry that involves multiple atoms like axial helecene. As shown in Fig. 8.5, the molecule has no chiral centers but is “optically active” (experimentally measured to be chiral) because of its helix which can be left- or right-handed.

8.14. Relevant Videos¶

8.14.1. Intro to GNNs¶

8.14.2. Overview of GNN with Molecule, Compiler Examples¶

8.15. Chapter Summary¶

Molecules can be represented by graphs by using one-hot encoded feature vectors that show the elemental identity of each node (atom) and an adjacency matrix that show immediate neighbors (bonded atoms).
Graph neural networks are a category of deep neural networks that have graphs as inputs.
One of the early GNNs is the Kipf & Welling GCN. The input to the GCN is the node feature vector and the adjacency matrix, and returns the updated node feature vector. The GCN is permutation invariant because it averages over the neighbors.
A GCN can be viewed as a message-passing layer, in which we have senders and receivers. Messages are computed from neighboring nodes, which when aggregated update that node.
A gated graph neural network is a variant of the message passing layer, for which the nodes are updated according to a gated recurrent unit function.
The aggregation of messages is sometimes called pooling, for which there are multiple reduction operations.
GNNs output a graph. To get a per-atom or per-molecule property, use a readout function. The readout depends on if your property is intensive vs extensive
The Battaglia equations encompasses almost all GNNs into a set of 6 update and aggregation equations.
You can convert xyz coordinates into a graph and use a GNN like SchNet

8.16. Cited References¶

DJL+20(1,2): Vijay Prakash Dwivedi, Chaitanya K Joshi, Thomas Laurent, Yoshua Bengio, and Xavier Bresson. Benchmarking graph neural networks. arXiv preprint arXiv:2003.00982, 2020.
BBL+17: Michael M Bronstein, Joan Bruna, Yann LeCun, Arthur Szlam, and Pierre Vandergheynst. Geometric deep learning: going beyond euclidean data. IEEE Signal Processing Magazine, 34(4):18–42, 2017.
WPC+20: Zonghan Wu, Shirui Pan, Fengwen Chen, Guodong Long, Chengqi Zhang, and S Yu Philip. A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems, 2020.
LWC+20(1,2): Zhiheng Li, Geemi P Wellawatte, Maghesree Chakraborty, Heta A Gandhi, Chenliang Xu, and Andrew D White. Graph neural network based coarse-grained mapping prediction. Chemical Science, 11(35):9524–9531, 2020.
YCW20: Ziyue Yang, Maghesree Chakraborty, and Andrew D White. Predicting chemical shifts with graph neural networks. bioRxiv, 2020.
XFLW+19: Tian Xie, Arthur France-Lanord, Yanming Wang, Yang Shao-Horn, and Jeffrey C Grossman. Graph dynamical networks for unsupervised learning of atomic scale dynamics in materials. Nature communications, 10(1):1–9, 2019.
SLRPW21: Benjamin Sanchez-Lengeling, Emily Reif, Adam Pearce, and Alex Wiltschko. A gentle introduction to graph neural networks. Distill, 2021. https://distill.pub/2021/gnn-intro. doi:10.23915/distill.00033.
XG18: Tian Xie and Jeffrey C. Grossman. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett., 120:145301, Apr 2018. URL: https://link.aps.org/doi/10.1103/PhysRevLett.120.145301, doi:10.1103/PhysRevLett.120.145301.
KW16: Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907, 2016.
GSR+17: Justin Gilmer, Samuel S Schoenholz, Patrick F Riley, Oriol Vinyals, and George E Dahl. Neural message passing for quantum chemistry. arXiv preprint arXiv:1704.01212, 2017.
LTBZ15: Yujia Li, Daniel Tarlow, Marc Brockschmidt, and Richard Zemel. Gated graph sequence neural networks. arXiv preprint arXiv:1511.05493, 2015.
CGCB14: Junyoung Chung, Caglar Gulcehre, KyungHyun Cho, and Yoshua Bengio. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:1412.3555, 2014.
XHLJ18(1,2): Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. How powerful are graph neural networks? In International Conference on Learning Representations. 2018.
LDLio19: Enxhell Luzhnica, Ben Day, and Pietro Liò. On graph classification networks, datasets and baselines. arXiv preprint arXiv:1905.04682, 2019.
MSK20: Diego Mesquita, Amauri Souza, and Samuel Kaski. Rethinking pooling in graph neural networks. Advances in Neural Information Processing Systems, 2020.
GZBA21: Daniele Grattarola, Daniele Zambon, Filippo Maria Bianchi, and Cesare Alippi. Understanding pooling in graph neural networks. arXiv preprint arXiv:2110.05292, 2021.
DRA21: Ameya Daigavane, Balaraman Ravindran, and Gaurav Aggarwal. Understanding convolutions on graphs. Distill, 2021. https://distill.pub/2021/understanding-gnns. doi:10.23915/distill.00032.
ZKR+17(1,2): Manzil Zaheer, Satwik Kottur, Siamak Ravanbakhsh, Barnabas Poczos, Russ R Salakhutdinov, and Alexander J Smola. Deep sets. In Advances in neural information processing systems, 3391–3401. 2017.
BHB+18: Peter W Battaglia, Jessica B Hamrick, Victor Bapst, Alvaro Sanchez-Gonzalez, Vinicius Zambaldi, Mateusz Malinowski, Andrea Tacchetti, David Raposo, Adam Santoro, Ryan Faulkner, and others. Relational inductive biases, deep learning, and graph networks. arXiv preprint arXiv:1806.01261, 2018.
SchuttSK+18(1,2,3): Kristof T Schütt, Huziel E Sauceda, P-J Kindermans, Alexandre Tkatchenko, and K-R Müller. Schnet–a deep learning architecture for molecules and materials. The Journal of Chemical Physics, 148(24):241722, 2018.
CW22: Sam Cox and Andrew D White. Symmetric molecular dynamics. arXiv preprint arXiv:2204.01114, 2022.
ZSX+18: Jiani Zhang, Xingjian Shi, Junyuan Xie, Hao Ma, Irwin King, and Dit-Yan Yeung. Gaan: gated attention networks for learning on large and spatiotemporal graphs. arXiv preprint arXiv:1803.07294, 2018.
HYL17: Will Hamilton, Zhitao Ying, and Jure Leskovec. Inductive representation learning on large graphs. In Advances in neural information processing systems, 1024–1034. 2017.
EPBM19: Federico Errica, Marco Podda, Davide Bacciu, and Alessio Micheli. A fair comparison of graph neural networks for graph classification. In International Conference on Learning Representations. 2019.
SMBGunnemann18: Oleksandr Shchur, Maximilian Mumme, Aleksandar Bojchevski, and Stephan Günnemann. Pitfalls of graph neural network evaluation. arXiv preprint arXiv:1811.05868, 2018.
KGrossGunnemann20(1,2): Johannes Klicpera, Janek Groß, and Stephan Günnemann. Directional message passing for molecular graphs. In International Conference on Learning Representations. 2020.
JES+20: Bowen Jing, Stephan Eismann, Patricia Suriana, Raphael JL Townshend, and Ron Dror. Learning from protein structure with geometric vector perceptrons. arXiv preprint arXiv:2009.01411, 2020.
Velivckovic22: Petar Veličković. Message passing all the way up. arXiv preprint arXiv:2202.11097, 2022.
BFO+21: Cristian Bodnar, Fabrizio Frasca, Nina Otter, Yuguang Wang, Pietro Lio, Guido F Montufar, and Michael Bronstein. Weisfeiler and lehman go cellular: cw networks. Advances in Neural Information Processing Systems, 34:2625–2640, 2021.
TZK21: Erik Thiede, Wenda Zhou, and Risi Kondor. Autobahn: automorphism-based graph neural nets. Advances in Neural Information Processing Systems, 2021.

7. Standard Layers

9. Input Data & Equivariances

deep learning for molecules & materials